Question 1208039: A golf ball is hit with an initial velocity of 130 feet per second at an inclination of 45° to the horizontal. In physics, it is established that the height h of the golf ball is given by the function
h(x) = [(-32x^2)/(130)^2] + x, where x is the distance that the golf ball has traveled.
How far was the ball hit?
I know that the question is asking to find x.
What is the set up?
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A golf ball is hit with an initial velocity of 130 feet per second at an inclination of 45°
to the horizontal. In physics, it is established that the height h of the golf ball
is given by the function h(x) = [(-32x^2)/(130)^2] + x, where x is the distance
that the golf ball has traveled.
How far was the ball hit?
I know that the question is asking to find x.
What is the set up?
~~~~~~~~~~~~~~~~~~~~~~~~~~
In this problem, the scene/(the stage where the events take place) is a horizontal line,
representing the Earth surface.
The ball starts its movement at the beginning of the coordinate system x= 0 at h(0) = 0
and finally falls at some x > 0, where h(x) is zero, again.
So, the setup equation to find the coordinate x, where the ball lands, is
h(x) = 0,
or
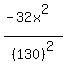 + +  = 0.
One root of this equation is x= 0, where the ball starts. You need the other root.
From this equation, the other root is
x = = 0.
One root of this equation is x= 0, where the ball starts. You need the other root.
From this equation, the other root is
x = 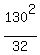 = 528.125 feet.
The ANSWER is: the ball lands at 528.125 feet from the start. = 528.125 feet.
The ANSWER is: the ball lands at 528.125 feet from the start.
Solved, with explanations.
|
|
|