Question 1207884: Show that the line containing the points (a, b)and (b, a), where a does not equal b ,is perpendicular to the line y = x. Also, show that the midpoint of (a,b)and (b,a) lies on the line y = x .
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
(a) Show that the line containing the points (a, b)and (b, a), where a does not equal b, is perpendicular to the line y = x.
(b) Also, show that the midpoint of (a,b)and (b,a) lies on the line y = x .
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
(a) The line, containing points (a,b) and (b,a), has the slope
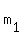 = = 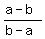 = -1.
The line y = x has the slope = -1.
The line y = x has the slope  = 1.
Since = 1.
Since 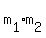 = 1*(-1) = -1, the numbers = 1*(-1) = -1, the numbers 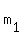 and and  are opposite reciprocal.
From this, we conclude that these two lines are perpendicular.
(b) The midpoint is ( are opposite reciprocal.
From this, we conclude that these two lines are perpendicular.
(b) The midpoint is (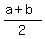 , ,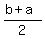 ).
Thus you see that x-coordinate of the midpoint is equal to its y-coordinate.
From this, we conclude that the midpoint lies on the line y = x. ).
Thus you see that x-coordinate of the midpoint is equal to its y-coordinate.
From this, we conclude that the midpoint lies on the line y = x.
At this point, the solution is complete, with all necessary explanations.
|
|
|