Question 1206279: Please give me a clear explanation and an example of an explicit and recursive equation Algebra 1 level.
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In arithmetic progression, the general formula for the next term is
 = =  + d.
This equation is a recursive equation example.
In arithmetic progression, the formula for the n-th term is + d.
This equation is a recursive equation example.
In arithmetic progression, the formula for the n-th term is
 = =  + d*(n-1).
It is an explicit formula example.
Roughly speaking, explicit formula allows calculating the term or the function explicitly.
Recursive formula allows calculating the next term of a sequence via the previous term (or several previous terms). + d*(n-1).
It is an explicit formula example.
Roughly speaking, explicit formula allows calculating the term or the function explicitly.
Recursive formula allows calculating the next term of a sequence via the previous term (or several previous terms).
---------------
If you want, you may look at this youtube lesson
https://www.youtube.com/watch?v=nH_z9mP--c0
about the same subject. They relate it to Algebra-I.
As more complicated/advanced popular example, there is a Fibonacci sequence.
You may read about it in this Wikipedia article
https://en.wikipedia.org/wiki/Fibonacci_sequence
This sequence was originated in XII century by Italian mathematician Fibonacci
who referred to studying a population of rabbits.
(the true story and applications are much more rich and interesting).
For this sequence, also there are recursive and explicit formulas.
So, arithmetic sequences, geometric sequences and the Fibonacci sequence are the closest examples,
but Fibonacci is just the level of 9th - 10th grades.
\\\\\\\\\\\\\\\\\\
O-o-o! There is one more example, quite simple.
It is the formula for the sum of interior angles of n-sided polygon
 = 180*(n-2) degrees. = 180*(n-2) degrees.
It is an explicit formula.
The recursive analogue is  = = 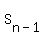 + 180. + 180.
The recursive formula can be deduced geometrically
by drawing a diagonal in an n-sided polygon, cutting a triangle.
Answer by math_tutor2020(3816)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Recursive example:

The top line indicates the 1st term is 5.
The next line says "whatever the nth term is, add 7 to it to get the (n+1)th term".
 = nth term = nth term
n is some positive integer 1,2,3,4,...
 = term just after the nth term = term just after the nth term
So,
 is the 2nd term is the 2nd term
 is the 3rd term is the 3rd term
 is the 4th term is the 4th term
And so on.
We generate the sequence 5, 12, 19, 26, ...
--------------------------------------------------------------------------
Since we're adding the same thing to each term, we can state this sequence is arithmetic.
 = first term = first term
 = common difference = common difference
The explicit closed form equation would be


Let's try n = 4





That matches the previous  value found through the recursive process. value found through the recursive process.
I'll let the student try other values of n. Make sure of course to only plug in positive integers.
There's pros and cons to both forms. If you wanted say the 99th term of this arithmetic sequence, then it would be tedious to follow the recursive route.
This is because you'd need the 98th term, but the 98th term needs the 97th term, and so on.
Use the explicit equation instead.
But the recursive method isn't always bad. It might be more intuitive to some students to see what is going on. For some students it might be easier to repeatedly add 7 to get to the desired term. The recursive form is generally practical for small values of n.
|
|
|