SOLUTION: Consider the following system of linear equations 𝑥 + 3𝑦 + 2𝑧 - 𝑤 = −1 −3𝑥 − 7𝑦 + (𝑝 − 6)𝑧 + 2𝑤 = 1 2𝑥 + 𝑝^2𝑧 + 𝑝𝑤 = 𝑞^2 wh

Click here to see ALL problems on Equations

Question 1205181: Consider the following system of linear equations
𝑥 + 3𝑦 + 2𝑧 - 𝑤 = −1
−3𝑥 − 7𝑦 + (𝑝 − 6)𝑧 + 2𝑤 = 1
2𝑥 + 𝑝^2𝑧 + 𝑝𝑤 = 𝑞^2
where 𝑝 and 𝑞 are real numbers.
Using Gaussian elimination, determine all possible values of 𝑝 and 𝑞 such that the system has no solution.
Answer by Edwin McCravy(20055) (Show Source):
You can put this solution on YOUR website!

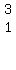
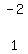
Write the augmented matrix for the given system of equations. A augmented matrix has no solution if a row has all 0's except for a non-zero element, say 1, for the rightmost element. For it would represent the equation 0x+0y+0z+0w=1. We try to get a row with all 0's except for a non-zero element for a rightmost element. 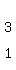Multiply row 1 by 3 and add to row 2: Multiply row 1 by -2 and add to row 3: Multiply row 2 by 3 and add to row 3: The bottom row will represent an equation with no solution if: If p=1, the first two equations will be true. The inequality will hold if 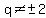Answer: , 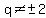Edwin