SOLUTION: Consider the following system of linear equations: 𝑥 + 3𝑦 + 2𝑧 − 𝑤 = −1 −3𝑥 − 7𝑦 + (𝑝 − 6)𝑧 + 2𝑤 = 1 2𝑥 + 𝑝^2𝑧 + 𝑝𝑤 = 𝑞^2

Algebra ->  Equations -> SOLUTION: Consider the following system of linear equations: 𝑥 + 3𝑦 + 2𝑧 − 𝑤 = −1 −3𝑥 − 7𝑦 + (𝑝 − 6)𝑧 + 2𝑤 = 1 2𝑥 + 𝑝^2𝑧 + 𝑝𝑤 = 𝑞^2       Log On


   

Question 1205169: Consider the following system of linear equations:
𝑥 + 3𝑦 + 2𝑧 − 𝑤 = −1
−3𝑥 − 7𝑦 + (𝑝 − 6)𝑧 + 2𝑤 = 1
2𝑥 + 𝑝^2𝑧 + 𝑝𝑤 = 𝑞^2
where 𝑝 and 𝑞 are real numbers.
Using Gaussian elimination, determine all possible values of 𝑝 and 𝑞 such that the system has infinitely many solutions with two free variables and solve the system.
Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!

The augmented matrix for that system of equations is:



Now if you had to find the row-reduced echelon form of that matrix by hand,
that would be a big chore. But these days, we are getting more and more
specialized calculators in sites online.  So we are having to do less and less
mathematical manipulations ourselves.  However, you can bet your sweet bippy
that sooner or later you're going to have to start paying out good money to
subscribe to these sites.  But while they're still free, get the row-reduced
echelon form of this matrix from this site, which hasn't started charging yet:

https://www.emathhelp.net/en/calculators/linear-algebra/reduced-row-echelon-form-rref-calculator/



This shows that:

 

So the system will always have a solution, and infinitely many solutions, as
long as none of those denominators equal 0. That is,

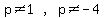matrix%281%2C3%2Cp%3C%3E1%2C%22%2C%22%2Cp%3C%3E-4%29.

There are 2 free variables, w and q, and there's almost a 3rd free variable,
because p is free to take on any value other than 1 and -4.  So p cannot be
considered totally free.

Edwin