Question 1204676: When two identical air pucks with repelling magnets are held together on an air table and released, they end up moving in opposite directions at the same speed, v. Assume the mass of one of the pucks is doubled and the procedure is repeated.
1. From Newton's third law, derive an equation that finds how the final speed of the double-mass puck compares with the speed of the single puck.
2. Calculate the speed of the double-mass puck if the single puck moves away at 0.36m/s.
Found 2 solutions by mananth, ikleyn:
Answer by mananth(16946)   (Show Source): (Show Source):
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
When two identical air pucks with repelling magnets are held together on an air table and released,
they end up moving in opposite directions at the same speed, v.
Assume the mass of one of the pucks is doubled and the procedure is repeated.
1. From Newton's third law, derive an equation that finds how the final speed
of the double-mass puck compares with the speed of the single puck.
2. Calculate the speed of the double-mass puck if the single puck moves away at 0.36m/s.
~~~~~~~~~~~~~~~~~~~
It is for the first time in my life I see such a problem and read these words "air pucks with repelling magnets".
So, my first step was to learn about it.
To do it, I asked Google, and Google provided me this link
https://www.amazon.com/Arbor-Scientific-P4-2155-Puck-Physics/dp/B000701C2I
from which I quickly learned the subject. So, I advise you to look at this link, too.
Next, I saw in the Internet another web-site, which tried to solve the problem, but did it incorrectly.
https://www.reddit.com/r/HomeworkHelp/comments/lx5rc/physics_101_problem/
Nevertheless, it gave me an idea on HOW TO approach this problem, and now I am ready to solve it for you.
Solution
First of all, since the problem tells about speeds, we must determine a coordinate system,
to which we will relate our observations.
It is a stationary observer, to which the system of two magnets, held together in their initial condition
is unmoved.
This system of two air pucks with repelling magnets, that are held together, has initial potential energy P.
If you do not understand, what is it - it is a mechanical work, which is needed to bring magnets close together.
When two identical air pucks are released, they move with the final speeds "v" in opposite directions
relative to our observer.
Hence, the system of two air pucks has the KINETIC ENERGY  = =  = = 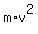 .
In the second scenario, the lighter air puck has the speed "u", while the heavier air puck has
the speed "w" relative to the same observer.
In this case, the kinetic energy of the system is .
In the second scenario, the lighter air puck has the speed "u", while the heavier air puck has
the speed "w" relative to the same observer.
In this case, the kinetic energy of the system is  = = 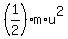 + + 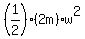 .
In both cases, kinetic energies are BOTH equal to the initial potential energy (due to the energy conservation law).
So, we write this equation for energies .
In both cases, kinetic energies are BOTH equal to the initial potential energy (due to the energy conservation law).
So, we write this equation for energies
 = = 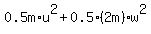 . (1)
I will cancel the common factor "m" (the mass), and my energy equation will lead to this equation . (1)
I will cancel the common factor "m" (the mass), and my energy equation will lead to this equation
 = = 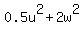 . (2)
So, now I have this equation (2) for THREE variables (unknowns) v, u and w.
Next, I will use the IMPULS CONSERVATION law (which is the same as the Newton third law). It says
m*u = (2m)*w.
After canceling the mass, it gives
u = 2w. (3)
Actually, this equality (3) just gives the answer to the problem' question
+------------------------------------------------+
| the speed of the doubled-mass air pucks |
| is half of the speed of the single air puck. |
+------------------------------------------------+
ANSWER. The speed of the doubled-mass air pucks is half of the speed of the single air puck. . (2)
So, now I have this equation (2) for THREE variables (unknowns) v, u and w.
Next, I will use the IMPULS CONSERVATION law (which is the same as the Newton third law). It says
m*u = (2m)*w.
After canceling the mass, it gives
u = 2w. (3)
Actually, this equality (3) just gives the answer to the problem' question
+------------------------------------------------+
| the speed of the doubled-mass air pucks |
| is half of the speed of the single air puck. |
+------------------------------------------------+
ANSWER. The speed of the doubled-mass air pucks is half of the speed of the single air puck.
At this point, the problem is just solved.
---------------------------
When I wrote to this point, I got understanding that my writing about kinetic energies
goes much further than the problem really asks (and, therefore, is irrelevant to this concrete problem).
Nevertheless, I decide to keep this writing in the hope that it will inspire somebody for further thinking.
------------------
Nice problem. Thanks for posting it.
It was a pleasure to me to think about it.
///////////////////
At the end, I'd like to make a note on the problem's formulation.
As question 1) is posed, it is unclear, to which scenario it really does relate:
does the question ask to find the ratio w to u, w/u, or the ratio w to v, w/v.
I found the ratio w/u.
But the problem becomes MUCH MORE interesting if asks to find w/v,
and for such solution the full consideration is needed of the impulse conservation
and energy conservation, as it is outlined in my solution.
In whole, the problem is nice, but it could be even better, if formulated more accurately.
\\\\\\\\\\\\\\\\\
By the way, there is more traditional way to pose similar question,
using a compressed spring between the masses, which is compressed at first and then is cut.
It is a traditional formulation in Physics, and such problems
are in use for Physics students just more than one or two hundred years.
|
|
|