Question 1203634: If there was a 30% discount and a 9% sales tax, what was the original price of a car that cost $4815?
What was the price after applying the discount of 30%?
How much taxes were paid?
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39616)   (Show Source):
Answer by ikleyn(52776)  (Show Source):
You can put this solution on YOUR website! .
If there was a 30% discount and a 9% sales tax, what was the original price of a car that cost $4815?
What was the price after applying the discount of 30%?
How much taxes were paid?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let x be the original price.
Then the price after 30% discount is x-0.3x = (1-0.3)x = 0.7x.
The general rule is that the sales tax applies to the price after the discount is applied.
So, when the 9% tax is applied, the buyer pays 1.09*0.7x = 0.763x.
Thus, to find x, you have this equation
0.763x = 4815.
From this equation, you get
x = 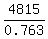 = 6310.62 dollars (rounded to the closest cent).
Thus, the original price of the car was 6310.62 dollars.
After applying the 30% discount, the price was 0.7*6310.62 = 4417.43 dollars (rounded to the closest cent).
The tax paid was 9% of $4417.43, or 0.09*4417.43 = 397.57 dollars.
Solved.
I suspect that in this problem, they do not look at cents, at all, and round everything to closest dollar.
|
|
|
