Question 1203631: Find A, B and C if 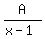 + + 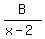 + + 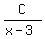 = = 
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3820)   (Show Source): (Show Source):
Answer by ikleyn(52944)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find A, B and C if 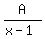 + + 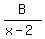 + + 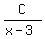 = = 
~~~~~~~~~~~~~~~
They want you find A, B, C from this given identity
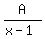 + + 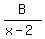 + + 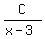 = =  This problem is, in some sense, a joking and entertainment Math problem.
Indeed, there are different ways/methods to solve it.
One way, shown by the other tutor, is direct and straightforward, but requires a lot of computations,
such as reducing the problem to a system of 3 linear equations and solving this system.
This way is like a torture and can only bring tears.
But there are other ways, so beautiful that you will smile learning them.
One of such method is my solution under this link
https://www.algebra.com/algebra/homework/expressions/expressions.faq.question.1196220.html
+--------------------------------------------------+
| The other method I will show right here. |
+--------------------------------------------------+
Multiply the given identity by (x-1). Then from the given identity (1), you will get this identity
A +
This problem is, in some sense, a joking and entertainment Math problem.
Indeed, there are different ways/methods to solve it.
One way, shown by the other tutor, is direct and straightforward, but requires a lot of computations,
such as reducing the problem to a system of 3 linear equations and solving this system.
This way is like a torture and can only bring tears.
But there are other ways, so beautiful that you will smile learning them.
One of such method is my solution under this link
https://www.algebra.com/algebra/homework/expressions/expressions.faq.question.1196220.html
+--------------------------------------------------+
| The other method I will show right here. |
+--------------------------------------------------+
Multiply the given identity by (x-1). Then from the given identity (1), you will get this identity
A + 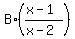 + + 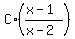 = = 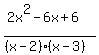 . (2)
In this identity, place x= 1. In its left side, you will get the second and the third addends zeroed
due to presence of the factor (x-1) in the numerator. Right side of (2) at x= 1 is . (2)
In this identity, place x= 1. In its left side, you will get the second and the third addends zeroed
due to presence of the factor (x-1) in the numerator. Right side of (2) at x= 1 is
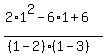 = = 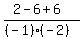 = = 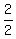 = 1.
Thus A = 1.
Let's find B in similar way. Multiply the given identity by (x-2). Then from the given identity (1),
you will get this identity = 1.
Thus A = 1.
Let's find B in similar way. Multiply the given identity by (x-2). Then from the given identity (1),
you will get this identity
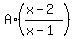 + B + + B +  = = 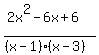 . (3)
In this identity, place x= 2. In its left side, you will get the first and the third addends zeroed
due to presence of the factor (x-2) in the numerator. Right side of (3) at x= 2 is . (3)
In this identity, place x= 2. In its left side, you will get the first and the third addends zeroed
due to presence of the factor (x-2) in the numerator. Right side of (3) at x= 2 is
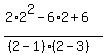 = =  = = 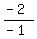 = -2.
Thus B = -2.
Find C in similar way. Multiply the given identity by (x-3). Then from the given identity (1),
you will get this identity = -2.
Thus B = -2.
Find C in similar way. Multiply the given identity by (x-3). Then from the given identity (1),
you will get this identity
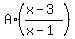 + + 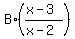 + C = + C =  . (4)
In this identity, place x= 3. In its left side, you will get the first and the second addends zeroed
due to presence of the factor (x-3) in the numerator. Right side of (4) at x= 3 is . (4)
In this identity, place x= 3. In its left side, you will get the first and the second addends zeroed
due to presence of the factor (x-3) in the numerator. Right side of (4) at x= 3 is
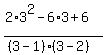 = = 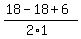 = = 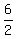 = 3.
Thus C = 3.
ANSWER. A = 1, B = -2, C = 3. = 3.
Thus C = 3.
ANSWER. A = 1, B = -2, C = 3.
Solved as a joke Math problem.
------------------
Next time, if you are given a similar functional identity of 10 addends with 10 unknown literal coefficients,
you do not need to reduce it to the system of 10 equations; you also do not need solve this system.
Simply apply this method and find the coefficients one after another, independently one from another,
spending one line for each coefficient.
|
|
|