Question 1203091: For the topic Linear equations inequalities create two unknowns (for example 10x+4y=72 and 4x+8y=48) but the intercept must be x=1 and y=19 or (1,19)
Found 3 solutions by Theo, ikleyn, math_tutor2020:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! your intercept must be equal to (1,19).
that means y = 19 when x = 1.
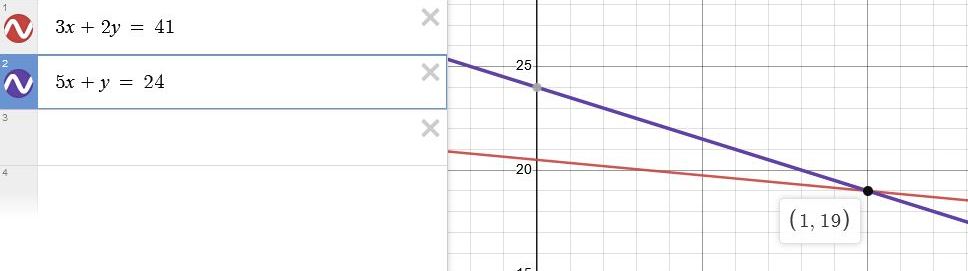
let your first equation be 3x + 2y = 3 + 38 = 41
let your second equation be 5x + y = 5 + 19 = 24
since these equations were created with x = 1 and y = 19, they should both intersect at (1,19).
the following graph confirms that they do.
Answer by ikleyn(52779)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
For the topic Linear equations inequalities create two unknowns (for example
10x+4y=72 and 4x+8y=48) but the intercept must be x=1 and y=19 or (1,19)
~~~~~~~~~~~~~~~~~~~~~
The formulation of the problem in your post is INCORRECT.
To be correct, it must use the term "intersection point" instead of the term "intercept",
mistakenly used in your post.
Do not scare (do not confuse) the readers using incorrect terms.
Answer by math_tutor2020(3816)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Any linear equation in standard form is Ax+By = C
A,B,C are integers.
For example: 2x+3y = 4
If we have the 2x+3y portion, then plugging in (x,y) = (1,19) leads to:
2x+3y
2*1+3*19
2+57
59
This means 2x+3y = 59 when (x,y) = (1,19)
Rephrased another way: (x,y) = (1,19) is a solution to 2x+3y = 59.
Another rephrasing: The point (1,19) is on the line 2x+3y = 59
Now let's generate the other equation.
Pick another two random integers.
Let's say we go for 5 and 6 to generate 5x+6y
Plug x = 1 and y = 19 into that expression
5x+6y
5*1+6*19
5+114
119
Therefore, 5x+6y = 119 when x = 1 and y = 19
In other words, the ordered pair (x,y) = (1,19) is a solution to 5x+6y = 119
The point (1,19) is on the line 5x+6y = 119.
We've demonstrated that (x,y) = (1,19) is a solution to both 2x+3y = 59 and 5x+6y = 119 simultaneously.
This point is on both lines at the same time.
This means the two lines intersect at (1,19).
Use Desmos, GeoGebra, TI83/84, or any graphing tool to visually confirm this.
A non-visual way to confirm is to use any of the following:- Substitution
- Elimination
- Matrix Row Reduction (either REF or RREF)
- Cramer's Rule
As the tutor Theo has shown using Desmos, there is another system of equations that yields the solution (x,y) = (1,19)
It turns out there are infinitely many systems possible. I encourage you to explore another possible system.
|
|
|