Question 1202383: Suppose that the marginal cost function of a handbag manufacturer is
C′(x)=0.375x2−x+200
dollars per unit at production level x (where x is measured in units of 100 handbags). Find the total cost of producing 10 additional units if 4 units are currently being produced.
Total cost of producing the additional units:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! my understanding is as follows:
the marginal cost function gives you the additional cost for the next unit.
it is not the cost of the next unit.
the cost for the next unit is the cost for the current unit plus the additional cost for the next unit.
the brightstorm video at https://www.brightstorm.com/math/calculus/applications-of-the-derivative/economics-marginal-cost-and-revenue-problem-1/ shows you what this means.
i also did those calculation in excel.
they tracked with the calculations in the video.
in the video, the cost function is 1800 + 10x + .02x^2
the marginal cost function is the derivative of that which is 10 + .04x
the video tells you that the cost for 500 units is 11800 and the cost for 501 units is 11830.02
the video tells you that the marginal cost for 500 units is 30 which is the additional cost to go from 500 units to 501 units.
you can see that this is approximately the same as the cost for 501 units minus the cost for 500 units which is 30.02.
the same concept applies to your problem.
the marginal cost function is c!(x) = .375*x^2 - x + 200
the cost function is c(x) = .125*x^3 - .5*x^2 + 200*x because the derivative of .125*x^3 - .5*x^2 + 200*x is 3*.125*x^2 -2*.5*x + 200
simplify that to get the derivative is .375*x^2 - x + 200.
you have:
c(x) = .125*x^3 - .5*x^2 + 200*x
c!(x) = .375*x^2 - x + 200
i'll do one calculation manually and let excel do the other calculations.
4 units are currently being produced.
10 additional units would get you to 14 units.
you are looking for the the sum of the additional cost for the 5th unit through the 14th unit.
that should be the sum of the results of the marginal cost function for x from 4 to 9.
that would be the approximate additional cost.
the actual additional cost would be the sum of the results of the cost function for x from c(5) minus c(4) to c(14) minus c(13).
to get the additional cost from c(4) to c(5), you would get:
c(4) = .125*4^3 - .5*4^2 + 200*4 = 800
c(5) = .125*5^3 - .5*5^2 + 200*5 = 1003.125
c(5) minus c(4) = 1003.125 minus 800 = 203.125
c'(4) = .375*4^2 - 4 + 100 = 200 = 202
you can see that c'(4) is an approximation of c(5) - c(4).
i used excel to to do the calculations from c(4) to c(14).
the results are shown below.
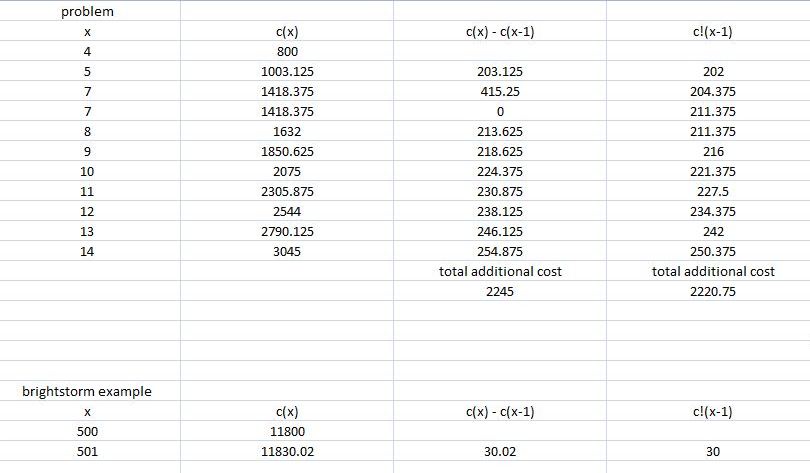
what excel shows you is that the sum of the additional costs from c(4) to (c(14) are equal to 2245, while the sum of the marginal costs from c'(4) to c'(13) are equal to 2220.75.
they're not the same, but they're close to each other.
c'(x-1) is an approximation of c(x) - c(x-1).
the answer is that the actual additional cost to go from 4 units to 14 units would be c(14) minus c(4) = .125*14^3 - .5*14^2 + 200*14 minus .125^4^3 - .5*4^2 + 200*4.
this is equal to 3045 minus 800 = 2245 as shown in excel.
since you were given c'(x), you have to find c(x) to get the actual additional costs.
once you had derived c(x) from x'(x), you you simply take c(14) minus c(4) to get the actual additional cost.
if you were just working with the marginal cost function, and didn't derive the cost function from that, then the additional cost would be the sum of the c'(4) through c'(9).
the sum of that approximation would be equal to 2220.75.
it's not 2245, but it's pretty close.
in this particular case, it was easier to find the actual additional cost rather than the approximate aqdditional cost, because the actual additional cost turned out to be c(14) - c(4), while the approximate additional cost was the sum of c'(4) to c'(9).
this is my understanding of the problem which may or may not be correct.
if it is correct, then your solution should be that:
the actual additional cost is 2245.
the approximate additional cost is 2220.75.
the brightstorm example is my calculations from the video.
i used that to test whether i was calculating the brightstorm video correctly.
it appears that i was.
you can just disregard that.
i forgot to remove it before publishing the results from excel.
|
|
|