Question 1201936: If p + 1/p = 5 and p does not equal 0, which of the following is a possible value of p - 1/p ?
(A) sqrt(25)
(B) sqrt(24)
(C) sqrt(23)
(D) sqrt(22)
(E) sqrt(21)
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If p + 1/p = 5 and p does not equal 0, which of the following is a possible value of p - 1/p ?
(A) sqrt(25)
(B) sqrt(24)
(C) sqrt(23)
(D) sqrt(22)
(E) sqrt(21)
~~~~~~~~~~~~~~~~~~
If  + + 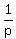 = 5, then by squaring
p^2 + 2 + = 5, then by squaring
p^2 + 2 + 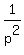 = 25
p^2 + = 25
p^2 + 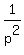 = 25 - 2 = 23
p^2 - 2 + = 25 - 2 = 23
p^2 - 2 + 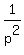 = 23 - 2 = 21 = 23 - 2 = 21
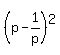 = 21 = 21
 - - 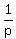 = +/- = +/-  .
That is all that we can state about .
That is all that we can state about  - - 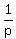 .
We can not state that it is necessary positive: it can be either positive .
We can not state that it is necessary positive: it can be either positive  or negative or negative 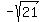 . .
--------------
You can check my solution and my statement directly.
From the given equation, it implies p^2 - 5p + 1 = 0,
giving the solutions 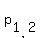 = = 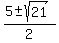 , that are either 4.791287847 or 0.208712153. , that are either 4.791287847 or 0.208712153.
First value gives p - 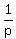 = 4.582575695 = = 4.582575695 =  . .
Second value gives p - 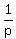 = -4.582575695 = = -4.582575695 = 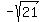 . .
So, what we can state definitely, is that (A), (B), (C) and (D) never may happen;
of listed options, only (E) may happen.
But for completeness, also  - - 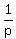 = = 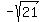 may happen, too, in addition to options listed in the problem's list. may happen, too, in addition to options listed in the problem's list.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: Choice (E) sqrt(21)
Explanation:
Square both sides of the given equation
p+ (1/p) = 5
[ p+ (1/p) ]^2 = 5^2
[ p+ (1/p) ][ p+ (1/p) ] = 25
p*p + p*(1/p) + (1/p)*p + (1/p)(1/p) = 25 .... FOIL rule
p^2 + 1 + 1 + (1/p)^2 = 25
p^2 + 2 + (1/p)^2 = 25
p^2 + (1/p)^2 = 23
I'll refer to this equation as eq2 for a substitution step later on.
Let q = p - (1/p)
Square both sides to see what happens
p - (1/p) = q
[ p - (1/p) ]^2 = q^2
p*p + p*(-1/p) + (-1/p)*p + (-1/p)(-1/p) = q^2
p^2 - 1 - 1 + (1/p)^2 = q^2
p^2 - 2 + (1/p)^2 = q^2
p^2 + (1/p)^2 - 2 = q^2
[ p^2 + (1/p)^2 ] - 2 = q^2
[ p^2 + (1/p)^2 ] - 2 = q^2
[ 23 ] - 2 = q^2 ......... substitution; use eq2
21 = q^2
q^2 = 21
q = sqrt(21)
p - (1/p) = sqrt(21)
------------------------------
Another approach would be to solve the equation p + (1/p) = 5 for p
p + (1/p) = 5
p * [ p + (1/p) ] = p*5
p^2 + 1 = 5p
p^2 - 5p + 1 = 0
Use the quadratic formula to find these two roots
p = (5 + sqrt(21))/2
p = (5 - sqrt(21))/2
Then use either root to compute p - (1/p)
I'll let you do these steps.
Hint:
If p = (5+sqrt(21))/2, then 1/p = (5 - sqrt(21))/2 after rationalizing the denominator.
A similar situation happens when p = (5 - sqrt(21))/2
|
|
|