Question 1201398: Jennifer, Grace, and Janet played Computer games. Jennifer won 30% of the total games, Grace 25%, and Janet 45%. There were no ties. What is the least possible number of the games that Jennifer won?
Found 4 solutions by josgarithmetic, greenestamps, ikleyn, math_tutor2020:
Answer by josgarithmetic(39632)   (Show Source): (Show Source):
Answer by greenestamps(13216)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I have no idea what question the other tutor was answering...!
The number of games the three players won are in the ratio 30:25:45.
Simplified to lowest terms, that ratio is 6:5:9, so the least possible number of games Jennifer won is 6.
ANSWER: 6
Answer by ikleyn(52944)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Jennifer, Grace, and Janet played Computer games.
Jennifer won 30% of the total games, Grace 25%, and Janet 45%.
There were no ties. What is the least possible number of the games that Jennifer won?
~~~~~~~~~~~~~~~~~~
The solution by @josgarithmetic is INCORRECT.
There is nothing farther from the correct solution, than that from his post.
For correct solution, see my post below.
From the context, the number of games in this problem is positive integer number.
They want you find the minimal positive integer number N such that
30% of N is integer number; 25% of N is integer number and 45% of N is integer number.
In other words, they want  of N be integer; of N be integer;  of N be integer and of N be integer and 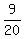 of N be integer.
It is not difficult to get (to guess, to tumble to - use any word) that N then is integer number 20.
Then the least possible number of the games that Jennifer won is 30% of 20, or 6. ANSWER of N be integer.
It is not difficult to get (to guess, to tumble to - use any word) that N then is integer number 20.
Then the least possible number of the games that Jennifer won is 30% of 20, or 6. ANSWER
Solved.
Answer by math_tutor2020(3820)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The percentages add to 100%, so let's say 100 games total had been played.
Each percentage corresponds to the whole number value shown here- Jennifer won 30 games
- Grace won 25 games
- Janet won 45 games
Simply erase the percent sign.
Divide each value over 100 and reduce the fraction.- Jennifer: 30/100 = (10*3)/(10*10) = 3/10
- Grace: 25/100 = (25*1)/(25*4) = 1/4
- Janet: 45/100 = (5*9)/(5*20) = 9/20
The reduced fractions are
3/10, 1/4, 9/20
The LCD is 20, so let's rewrite each denominator in terms of the LCD- Jennifer: 3/10 = (3*2)/(10*2) = 6/20
- Grace: 1/4 = (1*5)/(4*5) = 5/20
- Janet: 9/20 = 9/20
If 20 games were played, then,- Jennifer won 6/20 of those games. She won 6 games.
- Grace won 5/20 of those games. She won 5 games.
- Janet won 9/20 of those games. She won 9 games.
This scenario represents the fewest number of games played.
This is because the nature of the LCD is to go for the lowest denominator, i.e. lowest number of games in this case.
Answer: 6
This method is probably a bit more convoluted, so it might be more effective to use another route.
But it's always a good idea to have multiple pathways.
|
|
|