The line 2x-y+2 = 0 can be written in y = mx+b (m=slope, b=y-intercept) form:
y = 2x + 2
By inspection, the slope is 2
A line perpendicular to a line with slope m has slope -1/m. So for the above line, a line perpendicular to it has slope -1/2
For the curve  you can find the slope at any point by taking the derivative:
you can find the slope at any point by taking the derivative:  or
or 
The value of the derivative dy/dx at a given x, is the the slope of the tangent of 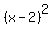 at x.
at x.
You are looking for x such that dy/dx = 2x - 4 = -1/2
Solving for x: 2x = -1/2 + 8/2 = 7/2 ---> x = (7/2)/2 = 7/4
At x = 7/4, y is 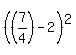 =
=  =
=  = 1/16
= 1/16
Thus, the point (7/4, 1/16) on  has a tangent perpendicular to the line y = 2x + 2.
has a tangent perpendicular to the line y = 2x + 2.
This illustrates the situation:
