SOLUTION: Using the chain rule, show that the following statements are always true: a) If f(x) is an odd function then f'(x) is an even function b) If f(x) is an even function then f'

Algebra ->  Equations -> SOLUTION: Using the chain rule, show that the following statements are always true: a) If f(x) is an odd function then f'(x) is an even function b) If f(x) is an even function then f'      Log On


   

Question 1200824: Using the chain rule, show that the following statements are always true:
a) If f(x) is an odd function then f'(x) is an even function
b) If f(x) is an even function then f'(x) is an odd function
Answer by Edwin McCravy(20055) About Me  (Show Source):
You can put this solution on YOUR website!
g(x) is an even function if and only if g(-x) = g(x)
g(x) is an odd function if and only if g(-x) = -g(x)
a) If f(x) is an odd function then f'(x) is an even function

f%28-x%29=-f%28x%29

Take derivatives of both sides:

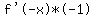
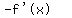
%22f%27%28-x%29%2A%28-1%29%22%22%22=%22%22%22-f%27%28x%29%22

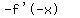
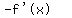%22-f%27%28-x%29%22%22%22=%22%22%22-f%27%28x%29%22

Divide both sides by -1

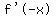
%22f%27%28-x%29%22%22%22=%22%22%22f%27%28x%29%22

So f'(x) is an even function.

-----------------------------------------------------------------
b) If f(x) is an even function then f'(x) is an odd function

f%28-x%29=-f%28-x%29

Take derivatives of both sides:

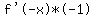
%22f%27%28-x%29%2A%28-1%29%22%22%22=%22%22%22-f%27%28-x%29%2A%28-1%29%22

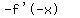
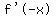%22-f%27%28-x%29%22%22%22=%22%22%22f%27%28-x%29%22

Divide both sides by -1

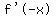
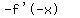%22f%27%28-x%29%22%22%22=%22%22%22-f%27%28-x%29%22

So f'(x) is an odd function.

Edwin