Question 1200591: If p=6q-r and t=3q+r , find p in terms of r and t .
What I did :
I first did r subject of formula:
3q+r=t
r=t-3q
Then I substituted the r in the other equation :
p=6q-(t-3q)
p=6q-t+3q
p=9q-t
But the correct answer is :p=2t-3r, how is this supposed to be worked out please?
Found 3 solutions by ikleyn, Theo, greenestamps:
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
If p=6q-r and t=3q+r , find p in terms of r and t .
~~~~~~~~~~~~~~~~
We should exclude q from p=6q-r, using the second equation t=3q+r.
So, from t=3q+r we find q= 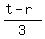 and then substitute it into
the first equation, replacing q there. We get then
p = 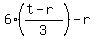 = 2*(t-r) - r = 2t - 2r - r = 2t - 3r,
exactly as your answer says.
Solved, with complete explanations.
Answer by Theo(13342)  (Show Source):
You can put this solution on YOUR website! start with p = 6q - r and t = 3q + r
solve for q in both equations to get:
q = (p + r) / 6 and q = (t - r) / 3
since they are both equal to q, set them equal to each other to get:
(p + r) / 6 = (t - r) / 3
multiply both sides of the equation by 6 to get:
p + r = 2 * (t - r)
simplify to get:
p + r = 2t - 2r
subtract r from both sides of the equation to get:
p = 2t - 3r
you needed to eliminate q from the equations.
that was done by solving for q in both equations.
you then used what q was equivalent to in each equation rather than q itself.
that eliminated q from both equations and left p and t and r.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
The given information shows p and t in terms of q and r, and it asks for p in terms of r and t. That means you need to eliminate q.
You eliminated p to get p in terms of q and t. You did that correctly -- but it was not what the question asked for.
The given equations are
p = 6q - r
t = 3q + r
By standard algebraic processes, to eliminate q you could solve one of the equations for q and substitute in the other equation.
But seeing that one equation has "6q" and the other has "3q", you can do the elimination more easily.
Multiply the second equation by 2 so that both equations have "6q":
p = 6q - r
2t = 6q + 2r
Now solve one of the equations for "6q" and substitute the expression for 6q in the other equation.
6q = p + r
2t = (p+r)+2r = p + 3r
And then solve for p
2t = p + 3r
p = 2t-3r
|
|
|
