SOLUTION: Assume that f(x) is continuous everywhere and lim (as x approaches to 4) (f(x)+2)/(x-4) = 11 What is the equation of the tangent line to y=f(x) and at what point (x,y) does it

The question is badly worded, because unless a continuous function is a linear
function, there are infinitely many tangent lines, not just one tangent line as
the words "the tangent line" here seems to imply.

The question should be:

"From the given information, is there a point at which we can determine the
equation of the tangent line? If so what is that point and what is the equation
of the tangent line at that point."



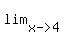
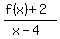
Since the denominator is 0 when x=4, the numerator must also = 0 when x=4.
Therefore,

f(4)+2 = 0
  f(4) = -2

Therefore, we know that (4,-2) is a point on f(x).

Since both the numerator and denominator of 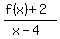 both
approach 0 as x approaches 4, we know that L'Hopital's rule holds.  Therefore
the quotient of the derivatives of the numerator and denominator has the same
limit 11 as x approaches 4.



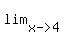
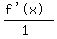
Therefore, f'(4) = 11, the slope of a tangent line at (4,-2)

So we know that at the point (4,-2) the slope of the tangent line is 11.

Using the point-slope formula for the equation of a line:







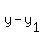
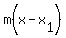
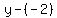
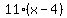
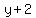
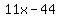
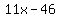 is the equation of the tangent line to

f(x) at the point (4,-2)

Edwin