SOLUTION: Evaluate using limit laws: Limit (as x approaches negative infinity) (x/sqrt(x^2-1)) Limit (as x approaches positive infinity) (x/sqrt(x^2-1))

Algebra ->  Equations -> SOLUTION: Evaluate using limit laws: Limit (as x approaches negative infinity) (x/sqrt(x^2-1)) Limit (as x approaches positive infinity) (x/sqrt(x^2-1))      Log On


   

Question 1200146: Evaluate using limit laws:
Limit (as x approaches negative infinity) (x/sqrt(x^2-1))
Limit (as x approaches positive infinity) (x/sqrt(x^2-1))
Answer by math_tutor2020(3816) About Me  (Show Source):
You can put this solution on YOUR website!

When x < 0, sqrt%28x%5E2%29+=+-x

When x > 0, sqrt%28x%5E2%29+=+x

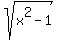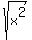For very large positive or negative values of x, sqrt%28x%5E2-1%29 approaches sqrt%28x%5E2%29.

This can be seen in the graph shown below
https://www.desmos.com/calculator/1llyy35ent
Desmos is a free graphing app.

The -1 at the end doesn't alter the radicand too much when x^2 is so very large.
Examples:
If x = 5, then x^2 = 25 and x^2-1 = 24
If x = 50, then x^2 = 2500 and x^2-1 = 2499
If x = 500, then x^2 = 250,000 and x^2-1 = 249,999
If x = 5000, then x^2 = 25,000,000 and x^2-1 = 24,999,999

This means 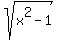sqrt%28x%5E2-1%29 approaches -x for large negative values of x.
Also, 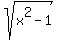sqrt%28x%5E2-1%29 approaches x for large positive values of x.


For very large negative values of x, 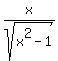x%2Fsqrt%28x%5E2-1%29 approaches x%2F%28-x%29+=+-1

For very large positive values of x, 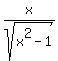x%2Fsqrt%28x%5E2-1%29 approaches x%2Fx+=+1

Therefore,

and


Verification using WolframAlpha
https://www.wolframalpha.com/input?i=x%2Fsqrt%28x%5E2-1%29+asymptotes

Verification using Desmos
https://www.desmos.com/calculator/hfq1eravms