Question 1199266: Solve for x.
x^2 + 3x + sqrt{x^2 + 3x} = 6
Moving x^2 + 3x to the right, I got this:
sqrt{x^2 + 3x} = -x^2 - 3x + 6
Squaring both sides leads to the following:
x^2 + 3x = x^4 + 6x^3 - 3x^2 - 36x + 36
I then moved every term on the left to the right side.
x^4 + 6x^3 - 4x^2 -39x + 36 = 0
Stuck here. . . .
According to the textbook, the answers for x are as follows: x = -4, x = 1.
Answer by ikleyn(52784)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Solve for x this equation x^2 + 3x + sqrt{x^2 + 3x} = 6.
~~~~~~~~~~~~~~~~~~~
The method to solve is introducing new variable.
(1) Notice that the expression under the square root must be non-negative
x^2 + 3x >= 0, or, equivalently, x*(x+3) >=0,
which means that either x >= 0 or x <= -3.
Thus the domain is (-oo,-3] U [0,oo).
Also, notice that we consider positive values of 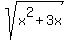 , only, so y >= 0.
(2) Introduce new variable y = , only, so y >= 0.
(2) Introduce new variable y = 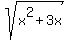 .
Then y^2 = x^2 + 3x, and the given equation takes the form
y^2 + y = 6, or, equivalently,
y^2 + y - 6 = 0
Factor left sides
(y+3)*(y-2) = 0
The roots are y= -3 ans y= 2.
Since we consider only positive values of y in this problem,
we analyse below the case y= 2 ONLY.
(3) If y= 2, then .
Then y^2 = x^2 + 3x, and the given equation takes the form
y^2 + y = 6, or, equivalently,
y^2 + y - 6 = 0
Factor left sides
(y+3)*(y-2) = 0
The roots are y= -3 ans y= 2.
Since we consider only positive values of y in this problem,
we analyse below the case y= 2 ONLY.
(3) If y= 2, then
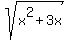 = 2.
Square both sides, simplify and find x
x^2 + 3x = 4
x^2 + 3x - 4 = 0
(x+4)*(x-1) = 0
Two roots are x= -4, x= 1. = 2.
Square both sides, simplify and find x
x^2 + 3x = 4
x^2 + 3x - 4 = 0
(x+4)*(x-1) = 0
Two roots are x= -4, x= 1.
Solved, and the obtained answer coincides with that in your textbook.
----------------
Memorize the method of the solution: it is introducing new variable
and accurate analysis of the domains of the variables x and y.
|
|
|