.
Step by step.
(1) Write several starting terms of the first series
cos(x) = 1 - 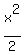 +
+  -
- 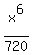 .
Replace here x with
.
Replace here x with  , since you want
, since you want  . You will get
. You will get
 = 1 -
= 1 -  +
+  -
-  . (1)
You should keep as many terms of this series to have at least the term with
. (1)
You should keep as many terms of this series to have at least the term with 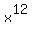 .
(2) Write several starting terms of the second series
.
(2) Write several starting terms of the second series
 =
=  -
- 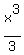 +
+ 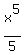 .
Replace here x with
.
Replace here x with  , since you want
, since you want  . You will get
. You will get
 =
=  -
-  +
+  . (2)
You should keep as many terms of this series to have at least the term with
. (2)
You should keep as many terms of this series to have at least the term with 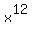 .
(3) Using (1) and (2), form
.
(3) Using (1) and (2), form  +
+  -
-  . You will get
. You will get
 +
+  -
-  = 1 -
= 1 -  +
+  -
-  +
+  -
-  +
+  - 1 =
= some terms will cancel; other will remain; I will keep the remaining terms with
- 1 =
= some terms will cancel; other will remain; I will keep the remaining terms with 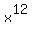 . It gives
=
. It gives
=  . The other terms have x in degrees HIGHER than 12.
(4) After dividing by
. The other terms have x in degrees HIGHER than 12.
(4) After dividing by 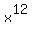 , I have
, I have  plus other terms with x of degree higher than 1.
When calculating the limit at x--> 0, these terms produce 0 (zero), so they are not interesting to me.
(5) Thus I get the ANSWER: the sough limit at x --> 0 equals
plus other terms with x of degree higher than 1.
When calculating the limit at x--> 0, these terms produce 0 (zero), so they are not interesting to me.
(5) Thus I get the ANSWER: the sough limit at x --> 0 equals  .
.
Solved.
Is everything clear to you ?