Question 1198925: The number 4^1000 - 1 is divisible by
a) 4 b) 5 c) 7 d) 13 e) 19
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
ANSWER: b) 5
Look at the pattern of remainders when 4^n-1 is divided by 5:
4^1-1 = 3; remainder when divided by 5 is 3
4^2-1 = 15; remainder when divided by 5 is 0
4^3-1 = 63; remainder when divided by 5 is 3
4^4-1 = 255; remainder when divided by 5 is 0
The pattern repeats forever; the remainder when 4^1000-1 is divided by 5 is 0.
You can find the similar patterns of remainders when 4^n-1 is divided by 7, 13, or 19; the length of the repeating patterns is such that 4^1000-1 will not be divisible by any of those other answer choices.
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The number 4^1000 - 1 is divisible by
a) 4 b) 5 c) 7 d) 13 e) 19
~~~~~~~~~~~~~~~
(a) Regarding (a), it is clear that the remainder of division 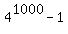 by 4 is -1,
which is the same as 3 mod(4); so, by 4 is -1,
which is the same as 3 mod(4); so, 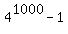 is not divisible by 4.
(b) Regarding (b), is not divisible by 4.
(b) Regarding (b), 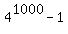 = = 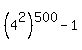 is divisible by is divisible by 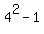 = 15;
so, = 15;
so, 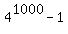 is divisible by 5.
(c, d, e) Regarding (c), (d) and (e), I prepared a table below, which shows the remainders
of division is divisible by 5.
(c, d, e) Regarding (c), (d) and (e), I prepared a table below, which shows the remainders
of division 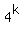 by 7, 13 and 19 respectively.
k by 7, 13 and 19 respectively.
k 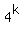 mod(7) mod(7) 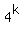 mod(13) mod(13) 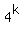 mod(13)
---------------------------------------------------------------
1 4 4 4
2 2 3 16
3 1 12 7
4 4 9 9
5 2 10 17
6 1 1 11
7 4 4 6
8 2 3 5
9 1 12 1
10 4 9 4
3 6 9 <<<---=== the length of the period.
The table shows that for each of these divisors, 7, 13, 19, the sequence of remainders
is periodical, as it should be.
Each period (in each column) starts from the very first term of the sequence.
For mod(7), the remainder 1 is every 3rd term of the sequence.
Since the index/(the degree) of 1000 is not a multiple of 3, mod(13)
---------------------------------------------------------------
1 4 4 4
2 2 3 16
3 1 12 7
4 4 9 9
5 2 10 17
6 1 1 11
7 4 4 6
8 2 3 5
9 1 12 1
10 4 9 4
3 6 9 <<<---=== the length of the period.
The table shows that for each of these divisors, 7, 13, 19, the sequence of remainders
is periodical, as it should be.
Each period (in each column) starts from the very first term of the sequence.
For mod(7), the remainder 1 is every 3rd term of the sequence.
Since the index/(the degree) of 1000 is not a multiple of 3, 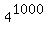 mod(7) is not 1;
hence, mod(7) is not 1;
hence, 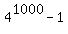 is not divisible by 7.
For mod(13), the remainder 1 is every 6th term of the sequence.
Since the index/(the degree) of 1000 is not a multiple of 6, is not divisible by 7.
For mod(13), the remainder 1 is every 6th term of the sequence.
Since the index/(the degree) of 1000 is not a multiple of 6, 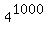 mod(13) is not 1;
hence, mod(13) is not 1;
hence, 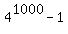 is not divisible by 13.
For mod(19), the remainder 1 is every 9th term of the sequence.
Since the index/(the degree) of 1000 is not a multiple of 9, is not divisible by 13.
For mod(19), the remainder 1 is every 9th term of the sequence.
Since the index/(the degree) of 1000 is not a multiple of 9, 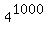 mod(19) is not 1;
hence, mod(19) is not 1;
hence, 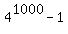 is not divisible by 19.
ANSWER. (a) is not divisible.
(b) is divisible.
(c) is not divisible.
(d) is not divisible.
(e) is not divisible. is not divisible by 19.
ANSWER. (a) is not divisible.
(b) is divisible.
(c) is not divisible.
(d) is not divisible.
(e) is not divisible.
Solved.
|
|
|