Question 1197454: please help my friend's homework hehe thankyou
Mike and gerry can finish building a doghouse in 4 hours. It would take mike 6 more hours that gerry to finish the job working alone. How long would it take each boy if each works alone?
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Mike and gerry can finish building a doghouse in 4 hours.
It would take mike 6 more hours  THAN gerry to finish the job working alone. THAN gerry to finish the job working alone.
How long would it take each boy if each works alone?
~~~~~~~~~~~~~~
Let  be the number of hours for gerry to cover the roof, working alone. be the number of hours for gerry to cover the roof, working alone.
If Mike works alone, he can complete this job in 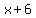 hours. hours.
Thus, in one single day Mike covers  part of the roof area, while gerry covers part of the roof area, while gerry covers  part of the roof area. part of the roof area.
Working together, Mike and gerry make 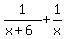 of the whole work in each single day. of the whole work in each single day.
Since they can cover the entire roof in 6 hours working together, the equation for the unknown value  is as follows: is as follows:
 . .
To simplify this equation, multiply both sides by 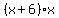 , then transfer all terms , then transfer all terms
from the right side to the left with the opposite signs, collect the common terms
and adjust the signs. In this way you get
 , ,
 , ,
 , ,
 , ,
You get the quadratic equation. It is factorable
(x-6)*(x+4) = 0
The equation has two roots:  and and  . .
The second root  makes no sense and we decline it. makes no sense and we decline it.
So, the potentially correct solution is  : gerry covers the roof in 6 hours working alone. : gerry covers the roof in 6 hours working alone.
Hence, Mike can complete the job in 6+6 = 12 hours.
Let us check it.
Since 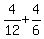 = =  = =  , this solution is correct. , this solution is correct.
Answer. gerry can finish the job in 6 hours working alone. Mike can complete the job in 12 hours.
Solved.
|
|
|