Question 1197452: please help me in my homework thankyouu!
A car traveling at a uniform speed reached its destination which is 400 kilometers away from the city. On the return trip, because of motor trouble, the speed is reduced to 10 miles per hour. This caused the car to stay on the road 2 hours longer. Find the speed of car
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A car traveling at a uniform speed reached its destination which is 400 kilometers away from the city.
On the return trip, because of motor trouble, the speed is reduced to 10 miles per hour.
This caused the car to stay on the road 2 hours longer. Find the speed of car
~~~~~~~~~~~~~
Let r be the faster speed, (r-10) be the slower speed.
Time moving with the speed "r" is 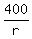 hours.
Time moving with the speed (r-10) is hours.
Time moving with the speed (r-10) is 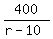 hours.
The difference of times gives an equation is hours.
The difference of times gives an equation is
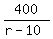 - - 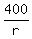 = 2 hours.
To solve, multiply both sides by r*(r-10). You will get
400*r - 400*(r-10)r = 2r*(r-10).
Simplify and find r
400r - 400r + 4000 = 2r^2 - 20r,
4000 = 2r^2 - 20r,
2000 = r^2 - 10r,
r^2 - 10r - 2000 = 0,
It can be factored
(r-50)*(r+40) = 0.
There are two roots, 50 and -40.
We reject the negative number and accept the positive one r = 50.
ANSWER. The faster rate is 50 km/h. The slower rate is 50-10 = 40 km/h.
CHECK. = 2 hours.
To solve, multiply both sides by r*(r-10). You will get
400*r - 400*(r-10)r = 2r*(r-10).
Simplify and find r
400r - 400r + 4000 = 2r^2 - 20r,
4000 = 2r^2 - 20r,
2000 = r^2 - 10r,
r^2 - 10r - 2000 = 0,
It can be factored
(r-50)*(r+40) = 0.
There are two roots, 50 and -40.
We reject the negative number and accept the positive one r = 50.
ANSWER. The faster rate is 50 km/h. The slower rate is 50-10 = 40 km/h.
CHECK. 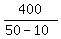 - - 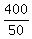 = 10 - 8 = 2 hours difference. ! Correct ! = 10 - 8 = 2 hours difference. ! Correct !
Solved.
----------------
The method to solve this and many other similar problems is to write "time" equation: it is your setup.
Then reduce this time equation to the standard form quadratic equation.
It can be solved by using the quadratic formula, or by factoring, if it is a lucky case.
At the end, you should be accurate, when you accept or decline one of the two possible roots:
if you decline, you should explain WHY.
|
|
|