Question 1197436: please help me in my assigments thankyouu!
A car traveling at a uniform speed reached its destination which is 400 kilometers away from the city. On the return trip, because of motor trouble, the speed is reduced to 10 miles per hour. This caused the car to stay on the road 2 hours longer. Find the speed of car
Found 3 solutions by josgarithmetic, ikleyn, math_tutor2020:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
please help me in my assigments thankyouu!
A car traveling at a uniform speed reached its destination which is 400 kilometers away from the city.
On the return trip, because of motor trouble, the speed is reduced to 10 miles per hour.
This caused the car to stay on the road 2 hours longer. Find the speed of car
~~~~~~~~~~~~~
Let r be the faster speed, (r-10) be the slower speed.
Time moving with the speed "r" is 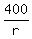 hours.
Time moving with the speed (r-10) is hours.
Time moving with the speed (r-10) is 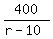 hours.
The difference of times gives an equation is hours.
The difference of times gives an equation is
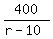 - - 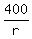 = 2 hours.
To solve, multiply both sides by r*(r-10). You will get
400*r - 400*(r-10)r = 2r*(r-10).
Simplify and find r
400r - 400r + 4000 = 2r^2 - 20r,
4000 = 2r^2 - 20r,
2000 = r^2 - 10r,
r^2 - 10r - 2000 = 0,
It can be factored
(r-50)*(r+40) = 0.
There are two roots, 50 and -40.
We reject the negative number and accept the positive one r = 50.
ANSWER. The faster rate is 50 km/h. The slower rate is 50-10 = 40 km/h.
CHECK. = 2 hours.
To solve, multiply both sides by r*(r-10). You will get
400*r - 400*(r-10)r = 2r*(r-10).
Simplify and find r
400r - 400r + 4000 = 2r^2 - 20r,
4000 = 2r^2 - 20r,
2000 = r^2 - 10r,
r^2 - 10r - 2000 = 0,
It can be factored
(r-50)*(r+40) = 0.
There are two roots, 50 and -40.
We reject the negative number and accept the positive one r = 50.
ANSWER. The faster rate is 50 km/h. The slower rate is 50-10 = 40 km/h.
CHECK. 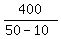 - - 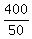 = 10 - 8 = 2 hours difference. ! Correct ! = 10 - 8 = 2 hours difference. ! Correct !
Solved.
----------------
The method to solve this and many other similar problems is to write "time" equation: it is your setup.
Then reduce this time equation to the standard form quadratic equation.
It can be solved by using the quadratic formula, or by factoring, if it is a lucky case.
At the end, you should be accurate, when you accept or decline one of the two possible roots:
if you decline, you should explain WHY.
Answer by math_tutor2020(3816)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I'll assume the part "the speed is reduced to 10 miles per hour" is supposed to be "the speed is reduced by 10 kilometers per hour".
This way the units match up, and a speed of 10 mph or 10 kph seems way too slow for a car.
If either of these assumptions are incorrect, then please let me know.
Let's organize what we know into a table
| Distance (km) | Rate (kph) | Time (hr) | | A to B | 400 | x | 400/x | | B to A | 400 | x-10 | 400/(x-10) |
Distance = rate*time
time = distance/rate
The time duration 400/(x-10) is larger since the speed x-10 is smaller compared to speed x.
Subtracting the time durations will get us a 2 hour gap due to the phrasing "This caused the car to stay on the road 2 hours longer".
longerTime - shorterTime = 2 hour gap
400/(x-10) - 400/x = 2
The first equation @josgarithmetic has set up is close, but the tutor has them incorrectly swapped.
Multiply both sides by x(x-10) and get everything to one side
400/(x-10) - 400/x = 2
x(x-10)(400/(x-10) - 400/x) = 2x(x-10)
400x - 400(x-10) = 2x(x-10)
400x - 400x+4000 = 2x^2-20x
4000 = 2x^2-20x
0 = 2x^2-20x-4000
2x^2-20x-4000 = 0
Compare this to ax^2+bx+c = 0
We find that
a = 2
b = -20
c = -4000
Let's use the quadratic formula





 or or 
 or or 
 or or 
The negative speed makes no sense, so we ignore it.
The only practical soluton is x = 50.
If x = 50, then x-10 = 50-10 = 40.
Check:
If you travel 400 km at a speed of 50 kph, then you take 400/50 = 8 hours
If you travel 400 km at a speed of 40 kph, then you take 400/40 = 10 hours
There is a 10-8 = 2 hour gap between the durations, so our answers are confirmed.
Answers:
On the way to the destination, the speed is 50 kph
On the return trip, the speed is 40 kph
|
|
|