.
Your starting equation is
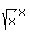 =
= 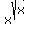 . (1)
One solution is x= 1 (obvious).
Indeed, left side is
. (1)
One solution is x= 1 (obvious).
Indeed, left side is 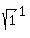 =
= 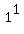 = 1.
Right side is equal to 1 due to the same reason.
Now I will assume that x =/= 1 and will look for other solutions.
Take logarithm base 10 of both sides of equation (1). You will get
= 1.
Right side is equal to 1 due to the same reason.
Now I will assume that x =/= 1 and will look for other solutions.
Take logarithm base 10 of both sides of equation (1). You will get
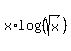 =
= 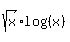 .
Divide both sides by log(x) (we can do it safely, since we consider x =/= 1.)
You will get
.
Divide both sides by log(x) (we can do it safely, since we consider x =/= 1.)
You will get
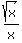 =
= 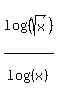 ,
or, equivalently,
,
or, equivalently,
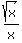 =
=  .
It implies
.
It implies
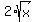 = x
and after squaring both sides,
4x =
= x
and after squaring both sides,
4x =  .
It implies
.
It implies
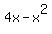 = 0
x*(4-x) = 0,
x = 0 or x= 4.
You can check that the root x= 0 works in the original equation, since then each side is equal to 1.
So, the remaining solutions to the problem are x= 0 and x= 4.
ANSWER. The given equation has three solutions x= 0, x= 1, and x= 4.
= 0
x*(4-x) = 0,
x = 0 or x= 4.
You can check that the root x= 0 works in the original equation, since then each side is equal to 1.
So, the remaining solutions to the problem are x= 0 and x= 4.
ANSWER. The given equation has three solutions x= 0, x= 1, and x= 4.
Solved.
To see that x= 0 is the solution, too, look at this plot below.
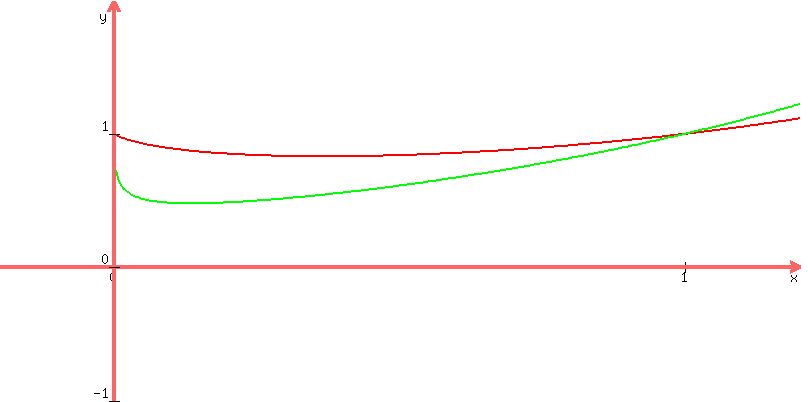 Plots y =
Plots y = 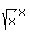 (red) and y =
(red) and y = 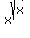 (green)
(green)