Question 1195869: This is a calculus question involving series. Can someone explain #13 on https://www.math.purdue.edu/php-scripts/courses/oldexams/serve_file.php?file=16200FE-F2019.pdf which is about true and false statements? My understanding is that I is true and II is false but I don't know about III and IV. Can someone give examples to show that they are true/false?
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I'll just put them in words:
I. If there is a finite area between an upper non-negative curve and
the x-axis, is there also a finite area between a lower non-negative
curve and the x-axis?
II. Take the special case. If f(x)=1 then does 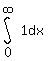 exist?
III. This is the same as I. If there is a finite area between an upper
non-negative curve and the x-axis, is there also a finite area between
a lower non-negative curve and the x-axis?
IV. If there is a finite area between a lower non-negative curve and
the x-axis, is there also a finite area between an upper curve and the
x-axis?
Edwin exist?
III. This is the same as I. If there is a finite area between an upper
non-negative curve and the x-axis, is there also a finite area between
a lower non-negative curve and the x-axis?
IV. If there is a finite area between a lower non-negative curve and
the x-axis, is there also a finite area between an upper curve and the
x-axis?
Edwin
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In this my post, I will not count the number of correct and wrong statements in the problem.
I will concentrate/focus entirely on statement III, ONLY.
Integral 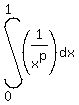 with p > 0 does exist (= converges) if and only if 0 < p < 1.
For the REFERENCE, see, for example,
https://www.sfu.ca/math-coursenotes/Math%20158%20Course%20Notes/sec_ImproperIntegrals.html
or your textbook/handbook (which, as I assume, is ALWAYS with you).
If the presumption in III is correct with p > 0, it means that 0 < p < 1.
Then, if q > p, there are two possibilities:
(a) q is still less than 1: q < 1, and then
integral with p > 0 does exist (= converges) if and only if 0 < p < 1.
For the REFERENCE, see, for example,
https://www.sfu.ca/math-coursenotes/Math%20158%20Course%20Notes/sec_ImproperIntegrals.html
or your textbook/handbook (which, as I assume, is ALWAYS with you).
If the presumption in III is correct with p > 0, it means that 0 < p < 1.
Then, if q > p, there are two possibilities:
(a) q is still less than 1: q < 1, and then
integral 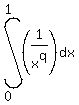 does exist (= converges).
(b) q >= 1, and then integral does exist (= converges).
(b) q >= 1, and then integral 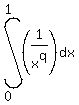 does NOT exist (= does NOT converge).
+-------------------------------------------------------------+
| THEREFORE, the statement III, as "if-then" statement, |
| considered for all possible cases, is FALSE. |
+-------------------------------------------------------------+
Sometimes (for some combinations of p and q), it is correct.
For other combinations, it is wrong.
+---------------------------------------------------------+
| But as a UNIVERSAL "if-then" statement, it is FALSE. |
+---------------------------------------------------------+
For example, the case p= 1/2, q= 2 is a COUNTER=EXAMPLE:
at p= 1/2, the presumption of III is correct, but the conclusion of III at q= 2 is WRONG. does NOT exist (= does NOT converge).
+-------------------------------------------------------------+
| THEREFORE, the statement III, as "if-then" statement, |
| considered for all possible cases, is FALSE. |
+-------------------------------------------------------------+
Sometimes (for some combinations of p and q), it is correct.
For other combinations, it is wrong.
+---------------------------------------------------------+
| But as a UNIVERSAL "if-then" statement, it is FALSE. |
+---------------------------------------------------------+
For example, the case p= 1/2, q= 2 is a COUNTER=EXAMPLE:
at p= 1/2, the presumption of III is correct, but the conclusion of III at q= 2 is WRONG.
Thus part (III) is solved and carefully/thoroughly explained.
-------------
Notice that interpretation given in the post by Edwin, does not work in case III.
It does not work, because the curve 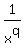 can be entirely below the curve can be entirely below the curve 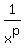
(as it happens at p= 1/2, q= 1/3, 0 < x < 1), when the integral does exists,
but it can be entirely above that curve (as it happens at p= 1/2, q= 2/3, 0 < x < 1), when the integral still exists,
or it can be entirely above that curve (as it happens at p= 1/2, q= 2, 0 < x < 1), when the integral does not exist.
 Plots y = 1/x^(1/2) (red), y = 1/x^(1/3) (green), y = 1/x^(2/3) (blue), y = 1/x^2 (magenta).
Plots y = 1/x^(1/2) (red), y = 1/x^(1/3) (green), y = 1/x^(2/3) (blue), y = 1/x^2 (magenta).
|
|
|