Question 1195707: An urn contains 2 one-dollar bills, 1 five-dollar bill and 1 ten-dollar bill. A player draws bills one at a time without replacement from the urn until a ten-dollar bill is drawn. Then the game stops. All bills are kept by the player. Determine:
(A) The probability of winning $16.
(B) The probability of winning all bills in the urn.
(C) The probability of the game stopping at the second draw.
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
An urn contains 2 one-dollar bills, 1 five-dollar bill and 1 ten-dollar bill.
A player draws bills one at a time without replacement from the urn
until a ten-dollar bill is drawn. Then the game stops.
All bills are kept by the player. Determine:
(A) The probability of winning $16.
(B) The probability of winning all bills in the urn.
(C) The probability of the game stopping at the second draw.
~~~~~~~~~~~~~~~~
In this post, I will solve part (A), only - - -
- - - in order for do not transform this nice problem into a mess.
(A) Winning $16 may happen only for these sequences of drawn dollars, step by step
(1,5,10) (with two possible instances for $1);
(5,1,10) (with two possible instances for $1).
Indeed, $10 must be drawn last, and the first and the second draws must be 1 and 5 in any order.
So, for winning $16, there are only these 4 winning sequences/outcomes.
From the other hand side, having $10 as the last drawing allows these sequences
(10); (1,10) (two instances, regarding two possible bills of $1); (5,10);
(1,1,10) (two instances, regarding two possible permutations of the two $1 bills);
(1,5,10) (two instances); (5,1,10) (two instances); (1,5,1,10) (two instances, regarding two possible permutations of the two $1 bills);;
(x,y,z,10), where x,y,z are 6 possible permutation of 3 bills $1, $1, and $5.
So, in all in the game, there are 1 + 2 + 1 + 2 + 2 + 2 + 2 + 6 = 18 possible outcome sequences;
of them, only 4 sequences are winning $16.
Thus the probability under question (A) is 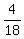 = =  . ANSWER . ANSWER
|
|
|