Question 1195393: Sketch the graph of a single function that has all of the properties listed.
a. Continuous and differentiable for all real numbers
b. f'(x)<0 on (-∞,-4) and(0,5)
c. f'(x)>0 on (-4,0) and (5,∞)
d. f''(x)>0 on (-∞,-1) and (2,∞)
e. f''(x)<0 on (-1,2)
f. f'(-4)=f'(5)=0
g.f''(x)=0 at (-1,11) and (2,10)
any help will be so appreciated this is the only question i have left on my homework and im stumped):
thank you so much in advance!
Answer by greenestamps(13216)   (Show Source): (Show Source):
You can put this solution on YOUR website!
--------------------------------------------------------------------
I need to rewrite my response -- in the question box the derivatives and second derivatives did not show up well, so originally I was working with all the wrong conditions....
--------------------------------------------------------------------
Note the problem does not ask you to find an equation -- it only asks you to sketch a graph.
But even with that I am still stumped, like you, because I don't think the given conditions can be met.
(1) Conditions b and c tell us that the graph has local minima at x=-4 and x=5, and a local maximum at x=0. Note that means that condition f is superfluous.
(2) Conditions d and e tell us the concavity changes from upwards to downwards at x=-1 and from downwards to upwards at x=2, so there are points of inflection at x=-1 and x=2.
So conditions b, c, d, e, and f give us 3 local extrema and 2 points of inflection, suggesting a polynomial of degree 4.
However, all of the given conditions can't be met with a polynomial of degree 4.
Given local extrema ONLY at x=-4, x=0, and x=5, the equation of the derivative is
f'(x) = 
Then the second derivative would be
f''(x) = 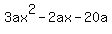
But that second derivative does not have zeros at x=-1 and x=2.
So it appears the best we can do with this problem is to ignore some of the conditions, and -- without trying to find an equation -- sketch a graph that is...
concave up from -infinity to -1, with a local minimum at -4;
concave down from -1 to 2, with a local maximum at 0; and
concave up from to infinity, with a local minimum at x=5.
----------------------------------------------------------------
Perhaps you will get other responses to your post from tutors who see the problem differently than I do....
|
|
|