SOLUTION: Find the value of the constant k that makes the function continuous. g(x)={2x^2-3x-20/x-4 if x≠4 {kx-15 if x=4 k= thanks for all your help!

First try to calculate the quadratic polynomial in the numerator at x= 4.


Its value is  2*4^2 - 3*4 - 20 = 2*16 - 12 - 20 = 32 - 12 - 20 = 0.


It tells you that the quadratic polynomial has the binomial (x-4) as a factor,
due to the Remainder theorem.


So, try to factorize the quadratic polynomial in the numerator.


You will get 2x^2 - 3x - 20 = (x-4)*(2x+5).


Therefore, the rationsl function  g(x) = 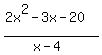 =  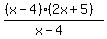= 2x+5.


It tells you that g(x), although has a hole at x= 4, nethertheless has a limit 2*4+5 = 13 at x ---> 4.


So we should take "k" in the expression kx-15 to get the value 13 at x=4:

    k*4 - 15 = 13,

or

    4k = 13 + 15 = 28

     k           = 28/4 = 7.


ANSWER.  k = 4.