SOLUTION: A boat travels 120 miles downstream in the same time as it travels 105 miles upstream. The speed of the current is 7 mph. What is the speed of the boat?

Algebra ->  Equations -> SOLUTION: A boat travels 120 miles downstream in the same time as it travels 105 miles upstream. The speed of the current is 7 mph. What is the speed of the boat?      Log On


   

Question 1193095: A boat travels 120 miles downstream in the same time as it travels 105 miles upstream. The speed of the current is 7 mph. What is the speed of the boat?
Answer by ikleyn(52780) About Me  (Show Source):
You can put this solution on YOUR website!
.


            There is NO such conception "speed of the boat", at all.

            There is a conception "speed of the boat relative to something", instead.

            In your case the question is about speed of the boat in still water. 


Let x be the speed of the boat in still water.


Then the speed of the boat moving downstream is (x+7) mph;

                           moving upstream   is (x-7) mph.


Write the "time" equation

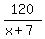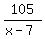    120%2F%28x%2B7%29 = 105%2F%28x-7%29


Cross-multiply, simplify and find x

    120*(x-7) = 105*(x+7)

      8*(x-7) =   7*(x+7)

      8x - 56 =   7x + 49

      8x - 7x =   49 + 56

         x    =     105 mph,   which is quite unrealistic.

You better throw this "problem" to the closest garbage bin.