Question 1191905: solve the inequality algebraically
2x/x-3 > 3x/2x+4
please solve with full answer thank you so much! :)
Found 3 solutions by MathLover1, greenestamps, math_tutor2020:
Answer by MathLover1(20849)   (Show Source):
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
The response from the other tutor uses the right process; but it doesn't show anything that teaches the student HOW to get the answer. And her solution set is not quite right; and her graph is rather strange....
The basic rule for solving an inequality like this is to get everything on one side of the inequality:
Combine fractions and write the expression in factored form.
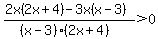
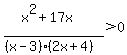
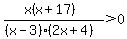
The "critical points" of the function are where the factors of the numerator or denominator are 0; from smallest to largest those points are x=-17, -2, 0, and 3.
Since the critical points are the only point where the function can be zero or undefined, they are the only points where the sign of the function can change. So those values divide the domain into intervals, on each of which the function value is either always positive or always negative.
Note that the function is defined at each critical point corresponding to a factor in the numerator, but it is undefined at each critical point corresponding to a factor in the denominator. So the function is defined at x=-17 and x=0 and undefined at x=-2 and x=3. Therefore, the intervals in the domain are the following:
(-infinity,-17]
[-17,-2)
(-2,0]
[0,3)
(3,infinity)
Now, having determined the intervals in the domain, most resources will tell you to pick a number in each interval to determine whether the sign in that interval is positive or negative.
However, that is more work than necessary. To make this part of the process easier, do the following:
(1) choose a "large" number -- greater than the largest critical point -- and determine the sign of the function; then
(2) "walk" along the x-axis to the left; each time you pass a critical point, one factor in the expression changes sign, which means the sign of the function will change.
Doing that, we find
(3, infinity): positive
[0,3): negative
(-2,0]: positive
[-17,-2): negative
(-infinity,-17): positive
ANSWER: The solution to the inequality is (-infinity,-17) U (-2,0] U (3,infinity)
-----------------------------------------------------------------------------------
Note: the above answer is not correct, because the original inequality was "greater than" instead of "greater than or equal to".
The correct solution is
(-infinity,-17) U (-2,0) U (3,infinity)
-----------------------------------------------------------------------------------
Here is a graph of the function, 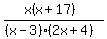 . Note there are zeros at x=-17 and x=0, where the numerator is zero, and asymptotes at x=-2 and x=3, where the denominator is zero.
Answer by math_tutor2020(3817)  (Show Source):
|
|
|
