Question 1191148: Given f(x) =-6x^2-8x
I) (f°f)(1)
Given g(x)= -12x-5
Find g^-1(5)
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! problem 1:
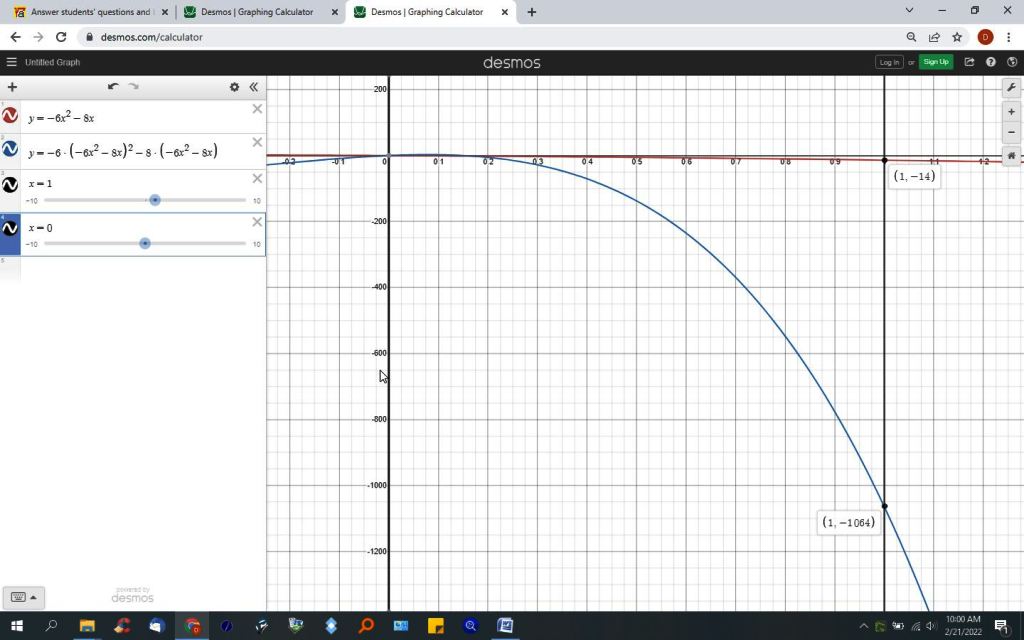
Given f(x) =-6x^2-8x, find f(f(1))
f(x) = -6x^2 - 8x
when x = 1, f(1) = -6 -8 = -14.
f(f(x)) = -6 * (-6x^2-8x)^2 - 8 * (-6x^2-8x)
when x = 1, -6x^2-8x = -14, therefore:
-f(f(1)) = -6 * (-14)^2 - 8 * -14 = -1064.
your solution is that f(f(1) = -1064.
this can be graphed.
the graph shows that the value of f(1) = -14 and the value of f(f(1)) = -1064.
here's the graph.
f(x) is in red.
f(f(x) is in blue
problem 2:
Given g(x)= -12x-5, find g^-1(5)
g^-1(x) is the inverse of g(x).
to find it, replace g(x) with y and then replace y with x and x with y and then solve for y.
start with:
g(x) = -12x-5
replace g(x) with y to get:
y = -12x-5
replace y with x and x with y to get:
x = -12y-5
switch sides to get:
-12y-5 = x
add 5 to both sides to get:
-12y = x+5
divide both sides by -12 to get:
y = -(x+5)/12
replace y with g^-1(x) to get:
g^-1(x) = -(x+5)/12
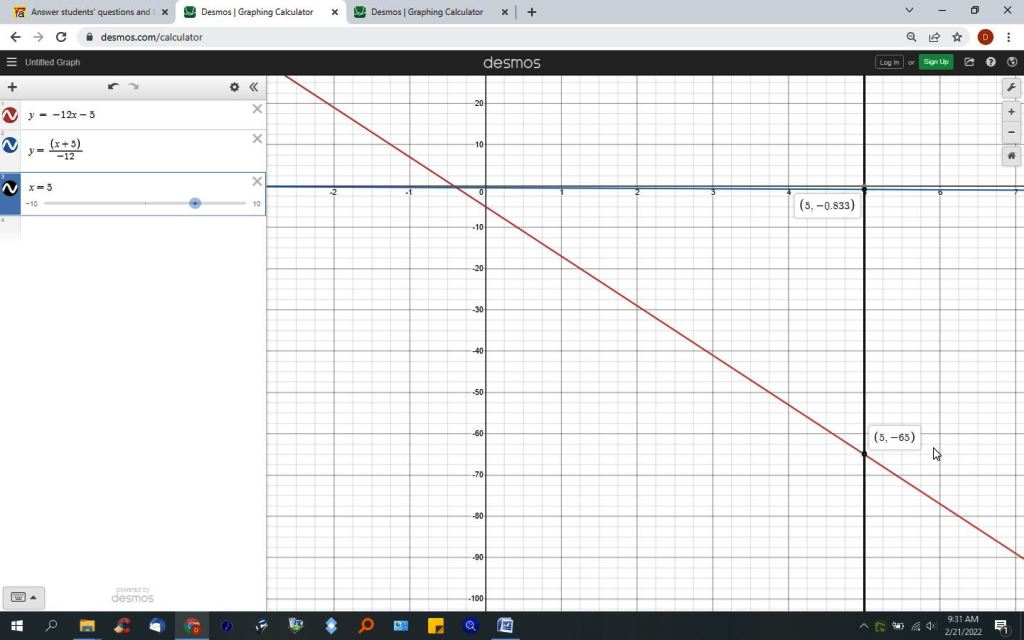
when x = 5, .....
g(x) = -12x-5 becomes -12 * 5 - 5 = -65
g^-1(x) = -(x+5)/12 = -10/12 = -.8333
g(x) and g^-1(x) can be graphed.
the graph is shown below.
in the graph, g(x) is replaced with y and g^-1(x) is replaced with y.
g(x) is in red.
g^-1(x) is in blue.
let me know if you have any questions or concerns.
theo
Answer by ikleyn(52777)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Given g(x)= -12x-5
Find g^-1(5)
~~~~~~~~~~~~~~~~~~~~~
To answer the question, you do not need to express the function g^(-1)(x) explicitly: it is an excessive unnecessary work.
What you really need is to solve equation g(x) = -5 and find x.
It is just enough and can be done in couple of lines.
To answer the question, you need to solve equation g(x) = 5, which is
12x - 5 = -5 and implies 12x = 0, x = 0.
ANSWER. x= 0.
Solved.
///////////////
If you want to get a right, clear and comprehensive explanation for each your problem/question,
NEVER submit more than one question/problem per post.
Otherwise, you will get some mess as an answer, which is difficult to read, to understand and to comment.
|
|
|