SOLUTION: When the positive integer n is divided by 7, the quotient is q and the remainder is 4. When 2n is divided by 7, the remainder is 1 and the quotient in terms of q, is a) q/2 b)

You just have to know how to check a division problem like

           QUOTIENT 
DIVISOR)   DIVIDEND
        ___
          ___    
          REMAINDER 
            
that you multiply the QUOTIENT by the DIVISOR and then add the
REMAINDER.  Then what you get must equal to the DIVIDEND.  


For instance, when the positive integer 57 is divided by 6,
the quotient is 57 and the remainder is 5

   57
6)347
  30
   47
   42
    5

To check the above: 
we multiply the quotient 57 by the divisor 6, getting 342.  Then
we add the remainder, 5, to 342 and we get 347, which is equal 
to the dividend.

Now, using that information, taking your first sentence:

>>...When the positive integer n is divided by 7, the quotient 
is q and the remainder is 4...<<

      q  
   7) n
     __
      4

So if we wanted to check that division as we did the numerical
one, we would multiply the quotient q by the divisor 7, getting
7q.  Then we would add the remainder, 4, to 7q and we'd get 7q+4,
which would be equal to the dividend n.  So we would have the 
equation:

   7q+4 = n  

Your second sentence says:

>>...When 2n is divided by 7, the remainder is 1 and the 
quotient...is ____...<< 

Let's let the quotient be x. Then we have:


      x  
   7)2n
     __
      1

So if we wanted to check that division, we would multiply the
quotient x by the divisor 7, getting 7x.  Then we would add the 
remainder, 1, to 7x and we get 7x+1, which would be equal to the 
dividend 2n.  So we would have the equation:

   7x+1 = 2n 

The words I left out of the second sentence were 

>>...in terms of q,...<<

So we have the two equations 

   7q+4 = n
   7x+1 = 2n

to solve for x the quotient, by substituting (7q+4) 
for n, gotten from the first equation, into the 
second equation:

   7x+1 = 2n

Rplace n by (7q+4)

   7x+1 = 2(7q+4)
   
then solving for x:

   7x+1 = 14q+8 

Add -1 to both sides

     7x = 14q+8-1
     7x = 14q+7

Divide every term on both sides by 7

     =  + 

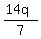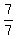      x = 2q+1

So the correct answer is (d).

Edwin