Question 1190924: A house is purchased for 1,000,000 in 2002. The value of the house is given by the exponential growth model A= 1,000,000e^(0.645)(t). Find t when the value of the house would be worth 5,000,000.
Found 2 solutions by ikleyn, Alan3354:
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A house is purchased for 1,000,000 in 2002.
The value of the house is given by the exponential growth model A= 1,000,000e^(0.645)(t).
Find t when the value of the house would be worth 5,000,000.
~~~~~~~~~~~~~~~~~~
So, we should find "t" from this equation
5000000 = 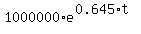 .
Divide both sides by 1000000. You will get
5 = .
Divide both sides by 1000000. You will get
5 = 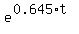 .
Take natural logarithm of both sides.
ln(5) = 0.645*t,
t = .
Take natural logarithm of both sides.
ln(5) = 0.645*t,
t =  = 2.495252577.
ANSWER. In 2.5 years, approximately.
CHECK. The annual growth factor is = 2.495252577.
ANSWER. In 2.5 years, approximately.
CHECK. The annual growth factor is 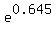 = = 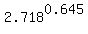 = 1.906, approximately.
In 2.5 years, the growth factor is = 1.906, approximately.
In 2.5 years, the growth factor is 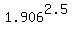 = 5.01, which confirms the answer. = 5.01, which confirms the answer.
Solved.
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! A house is purchased for 1,000,000 in 2002. The value of the house is given by the exponential growth model A= 1,000,000e^(0.645)(t). Find t when the value of the house would be worth 5,000,000.
----------------------------
5000000 = 1000000e^(0.645t)
e^(0.645t) = 5
Solve for t
|
|
|