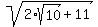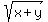SOLUTION: Given that x and y are integers and {{{ sqrt( 2 sqrt( 10 ) +11 ) = x+ sqrt( x+y ) }}}, find x-y

Your starting equality is

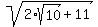     = x + 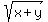.                 (1)


Square both sides. You will get

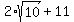     = x^2 + 2x*sqrt(x+y) + (x+y),

or, equivalently,

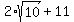     = x^2 + (x+y) + 2x*sqrt(x+y).    (2)


Since x and y are integer, we conclude

    11 = x^2 + x + y           (3)

    sqrt(10) = x*sqrt(x+y)     (4)


Square (4) again. You will get

    10 = x^2*(x + y).              (5)


10 = 1*10 = 2*5. Based on uniqueness of decomposition of the number 10 into the product of primes,

we conclude that equality (5) has a unique solution x= 1 and y= 9 in integer numbers.


Notice that equality  (3) is valid, too, with x= 1 and y= 9.


So, this pair (x,y) = (1,9) is the unique solution for equation (2), and, hence, for equation (1).


ANSWER.  x - y = 1 - 9 = -8.