Question 1189239: Given that 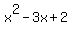 is a factor of is a factor of 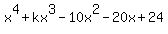 evaluate the sum of the four roots of the equation evaluate the sum of the four roots of the equation 
Found 2 solutions by ikleyn, MathTherapy:
Answer by ikleyn(52921)   (Show Source): (Show Source):
Answer by MathTherapy(10557)   (Show Source): (Show Source):
You can put this solution on YOUR website! Given that 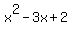 is a factor of is a factor of 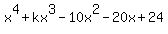 evaluate the sum of the four roots of the equation evaluate the sum of the four roots of the equation 
When factored,  = (x - 1)(x - 2). = (x - 1)(x - 2).
As  is a factor of is a factor of 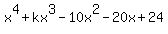 , x - 1 and x - 2 are also factors of , x - 1 and x - 2 are also factors of 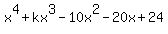 , which , which
means that x - 1 = 0, or x = 1, and x - 2 = 0, or x = 2. So, 2 of the roots of 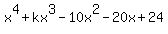 are 1 and 2. are 1 and 2.
Using either root, and the RATIONAL ROOT THEOREM, we find that k = 5.
The equation 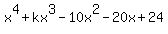 now becomes: now becomes: 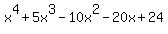 , and when POLYNOMIAL LONG-DIVISION and its , and when POLYNOMIAL LONG-DIVISION and its
factor,  are used, the other factor of the polynomial, are used, the other factor of the polynomial,  is derived. is derived.
And, when  is factored, its roots, from its factors x + 6 and x + 2, are - 6 and - 2. is factored, its roots, from its factors x + 6 and x + 2, are - 6 and - 2.
We now have roots: 1, 2, - 6, and - 2.
Therefore, the sum of the roots of 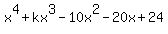 or or 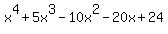 = 1 + 2 + (- 6) + (- 2) = - 5. = 1 + 2 + (- 6) + (- 2) = - 5.
|
|
|