.
Find the product(xy) if  and
and 
~~~~~~~~~~~~~~
Let 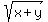 = p. (1)
Then first equation takes the form
p^2 + p - 20 = 0, or, factoring, (p+5)*(p-4) = 0. (2)
Its roots are p= -5 and p= 4.
Due to definition of p (1), we suppose, by default, that "p" is positive; so we choose p= 4.
Hence, x + y = 4^2 = 16. (3)
Let
= p. (1)
Then first equation takes the form
p^2 + p - 20 = 0, or, factoring, (p+5)*(p-4) = 0. (2)
Its roots are p= -5 and p= 4.
Due to definition of p (1), we suppose, by default, that "p" is positive; so we choose p= 4.
Hence, x + y = 4^2 = 16. (3)
Let 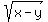 = q. (4)
Then second equation takes the form
q^2 + q - 12 = 0, or, factoring, (q+4)*(q-3) = 0. (5)
Its roots are q= -4 and q= 3.
Due to definition of q (4), we suppose, by default, that "q" is positive; so we choose q= 3.
Hence, x - y = 3^2 = 9. (6)
Thus we have these two equations
x + y = 16 (3)
x - y = 9 (6)
Solving by elimination, we get x =
= q. (4)
Then second equation takes the form
q^2 + q - 12 = 0, or, factoring, (q+4)*(q-3) = 0. (5)
Its roots are q= -4 and q= 3.
Due to definition of q (4), we suppose, by default, that "q" is positive; so we choose q= 3.
Hence, x - y = 3^2 = 9. (6)
Thus we have these two equations
x + y = 16 (3)
x - y = 9 (6)
Solving by elimination, we get x = 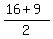 =
= 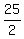 = 12.5; y = 16-x = 16-12.5 = 3.5.
THEREFORE, x*y = 12.5*3.5 = 43.75. ANSWER
= 12.5; y = 16-x = 16-12.5 = 3.5.
THEREFORE, x*y = 12.5*3.5 = 43.75. ANSWER
Solved.