SOLUTION: When 1 kg of salt is added to a solution and water, the solution becomes 33 1/3 % salt by mass. When 1 kg of water is added to the new solution, the resulting solution is 30% by m

Algebra ->  Equations -> SOLUTION: When 1 kg of salt is added to a solution and water, the solution becomes 33 1/3 % salt by mass. When 1 kg of water is added to the new solution, the resulting solution is 30% by m      Log On


   

Question 1187114: When 1 kg of salt is added to a solution and water, the solution becomes 33 1/3 % salt by mass. When 1 kg of water is added to the new solution, the resulting solution is 30% by mass. The percentage of salt in the original solution is? Can someone please solve this question?
Thanks in advance.
Found 3 solutions by josgarithmetic, ikleyn, greenestamps:
Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
The physical part of the description is wrong; a salt solution in water at ordinary room temperature is not higher than about 25 or 26 % salt.
Even at very high water temperatures, near boiling is needed to reach about 38%. Your description did not say anything about conditions of temperature.

1 kg of main ingredient added to a mixture of main ingredient plus carrier material gave 33&1/3 percent main ingredient.
Understand as a basic fact that 33&1/3 percent is 33&1/3 parts per hundred, or the same as 1/3. Since the entire description is based on mass,
this means your mixture up to this point is 1 kg of the main ingredient, and 2 kg of the carrier material. Those are THREE PARTS total by mass.
This means that the carrier material plus main ingredient at the beginning of the problem, HAD NO MAIN INGREDIENT. It was only the carrier material.

The problem description continued.
1 kg of carrier material was added to the mixture.
The result will then be:

mainIngredient%2FtotalMassMixture
%281%2Akg%29%2F%284%2Akg%29
%281%2F4%29
0.25
25 PERCENT

This is NOT 30% as the description stated.
Fix your problem description.

Answer by ikleyn(52780) About Me  (Show Source):
You can put this solution on YOUR website!
.
When 1 kg of salt is added to a solution and water, the solution becomes 33 1/3 % salt by mass.
When 1 kg of water is added to the new solution, the resulting solution is 30% by mass.
The percentage of salt in the original solution is? Can someone please solve this question?
~~~~~~~~~~~~~~~~~~~ 


Let x be the mass of salt (in kilograms), and let w be the mass of water (in kilograms) in the original solution.


Then from the problem's description, we have these equations for mass concentrations

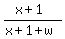    %28x%2B1%29%2F%28x%2B1%2Bw%29    = 1%2F3,      (1)

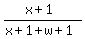    %28x%2B1%29%2F%28x%2B1%2Bw%2B1%29 = 3%2F10.     (2)


From these equations, we have further

    3(x+1)   = x + w  + 1                   

    10*(x+1) = 3(x + w + 2)                   


Continue transformations

     3x +  3 = x + w + 1                    

    10x + 10 = 3x + 3w + 6                


The standard form equations

    2x -  w = -2,      (3)

    7x - 3w = -4.      (4)


Apply the Elimination method.  For it, multiply equation (3) by 3;  keep equation (4) as is

    6x - 3w = -6,      (3')

    7x - 3w = -4.      (4')


From equation (4'), subtract equation (3').  You will get

    7x - 6x = -4 - (-6),  or  x = 2.


Then from equation (3),  w = 2x + 2 = 2*2 + 2 = 6.



So, the original solution was 6 kg of water and 2 kg of salt,

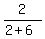and the original mass concentration of the solution was  2%2F%282%2B6%29 = 2%2F8 = 1%2F4 = 25%.    ANSWER

Solved.



Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


I read the problem differently than BOTH of the tutors from whom you have received responses. Here is what I read:

(1) You start with a solution of salt and water.
(2) After you add 1kg of salt to the original solution, you get an intermediate solution which is 33 1/3 % salt -- i.e, 1/3 salt.
(3) Then, after you add 1kg of water to the intermediate solution, the final solution is now 30% salt, or 3/10 salt.

Let's solve the problem by working backwards.

Let x/y represent the fraction of salt in the mixture; the mixture then consists of x parts salt and (y-x) parts water.

In the last step, when 1kg of water was added, the amount of salt remained unchanged. So we can determine the composition of the intermediate mixture by expressing the fractions 1/3 and 3/10 with the same NUMERATOR: 3/9 and 3/10.

With those two fractions, and knowing that 1kg of water was added, we can see that the intermediate mixture was 3kg salt and 9-3=6kgs water, and the final mixture was (still) 3kg salt but now 10-3=7kg water.

In the first step, the intermediate mixture was made by adding 1kg of salt to the original mixture. Since the intermediate mixture consisted of 3kg salt and 6kg water, the original mixture consisted of 2kg salt and 6kg water.

So the fraction of salt in the original mixture was 2/(2+6) = 2/8 = 1/4.

ANSWER: The fraction of salt in the original mixture was 25%