Question 1186694: How many integer solutions(a,b,c) make the equation a^2+b^2+c^2=121 true
Answer by ikleyn(52946)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
How many integer solutions(a,b,c) make the equation a^2+b^2+c^2=121 true
~~~~~~~~~~~~~~
The basic solutions are these 3 triples:
a b c
-------------------
0 0 11 (1)
2 6 9 (2)
6 6 7 (3)
1) Triple (1) creates 3 permutations, that are the solutions, too.
Playing with the signs, each of these permutations provides 2 triples, that are the solutions, too.
So, triple (1) produces 2*3 = 6 triples that are the solutions.
2) Triple (2) creates 6 permutations, that are the solutions, too.
Playing with the signs, we get 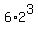 = 6*8 = 48 triples, that are the solutions, too.
So, triple (2) produces 48 triples that are the solutions.
3) Triple (3) creates 3 distinguishable permutations, that are the solutions, too.
Playing with the signs, each of these 3 distinguishable permutations provides 8 triples, that are the solutions, too.
So, triple (3) produces = 6*8 = 48 triples, that are the solutions, too.
So, triple (2) produces 48 triples that are the solutions.
3) Triple (3) creates 3 distinguishable permutations, that are the solutions, too.
Playing with the signs, each of these 3 distinguishable permutations provides 8 triples, that are the solutions, too.
So, triple (3) produces 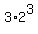 = 24 triples that are the solutions.
In all, there are 6 + 48 + 24 = 78 different integer triples that are the solutions. ANSWER = 24 triples that are the solutions.
In all, there are 6 + 48 + 24 = 78 different integer triples that are the solutions. ANSWER
Solved and explained.
|
|
|