He's right about the parentheses when typing numerators and denominators all
on one line. Otherwise, you can't tell where a numerator or denominator starts
and ends. Here is how you should have typed your problem:
((9x^2 - 64)/(x^2+7x+12)) ÷ ((3x^2+17x+24)/(x^2+6x+9))
Correct punctuation is even more important in math than in English. Anyways,
I'll assume what I think you meant to be a numerator and a denominator, and
where I think you meant for them to be.
----------------------------------------------------------
Even after we simplify the expression, we must make restrictions to make sure
that there are no numbers we could substitute for x that would cause the
original expression to be undefined by dividing by 0.
Therefore,
EACH TIME WE CANCEL ANY FACTOR, WE MUST MAKE A RESTRICTION THAT PREVENTS THE
CANCELED EXPRESSION FROM EVER BEING EQUAL TO ZERO. ALSO IN THE FINAL
SIMPLIFICATION, WE MUST MAKE A RESTRICTION THAT PREVENTS ITS DENOMINATOR
FROM BEING EQUAL TO ZERO.
÷ 
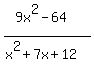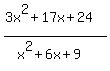Invert and multiply:
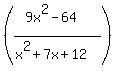
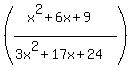Factor:
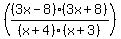
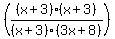We cancel the (3x+8)'s
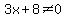
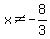We must indicate the restriction that x cannot equal -8/3.
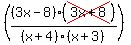
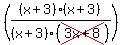We cancel one of the (x+3)'s and indicate the restriction
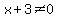
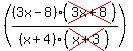
We cancel the other pair of (x+3)'s. [We've already indicated this restriction,
so we don't need to indicate it again.]
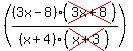
The final simplification is
We must also indicate that the denominator of the final simplification to
prevent it from ever being 0.
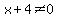
So putting in all the restrictions:
Edwin
