Question 1186200: Find the standard form of the equation of the ellipse with the given characteristics.
Center: (3, −8); a = 8c; foci: (3, −9), (3, −7)
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the standard form of the equation of the ellipse with the given characteristics.
Center: (3, −8); a = 8c; foci: (3, −9), (3, −7)
~~~~~~~~~~~~~~
Notice that the foci lie on vertical line x = 3.
It means that the major axis of the ellipse is vertical x= 3, parallel to y-axis,
and the minor axis is horizontal y= -8, parallel to x-axis.
The distance between the foci is 2c = -7 - (-9) = 2; hence, the linear eccentricity is half of this distance c = 2/2 = 1.
Further, the major semi-axis a = 8c = 8; hence, the minor semi-axis is b = 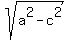 = = 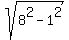 = =  .
Now we are ready to write the standard form equation of the ellipse .
Now we are ready to write the standard form equation of the ellipse
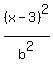 + + 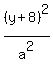 = 1,
or = 1,
or
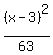 + + 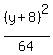 = 1. = 1.
Solved.
|
|
|