Question 1183388: An open lid tank to be made by concrete has width 50𝑐𝑚, inside capacity of 4000 𝑚3
and square base. Find the inner dimension of the tank with the minimum volume of
concrete.
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! The thickness of the open-lid tank is 50 cm = 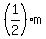 . Let the interior square base have a side of length . Let the interior square base have a side of length  meters. meters.
Also let the inner height be  m. m.
This then gives

since it is given that the inside capacity is 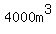 . .
For the exterior of the tank, the square base has a side of length
 meters, and a height of meters, and a height of 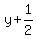 meters. meters.
The external volume is then
 , after substituting for , after substituting for  from the previous equation. from the previous equation.
==> 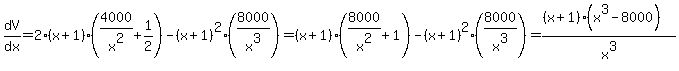 , ,
after simplifying the expression on the right side.
Setting  , we get , we get  . .
We cannot accept  since the domain of V is since the domain of V is 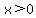 . .
Now if 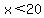 , ,  , and , and
when 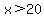 , , 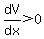 , so by the the 1st derivative test, , so by the the 1st derivative test,
there is a local minimum at  . Since it is the only critical . Since it is the only critical
point in the domain (0,  ), the minimum at ), the minimum at  is also is also
absolute minimum.
Therefore the inner dimensions of the tank are 20 m x 20 m x 10m. (The height is
 .) .)
|
|
|