Question 1183223: please help me solve
factorize 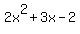
Found 3 solutions by Theo, MathTherapy, greenestamps:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! use the quadratic formula on this one.
quadratic formula is:
x = (-b plus or minus sqrt(b^2 - 4ac)) / 2a
in the equation 2x^2 + 3x - 2, ...
a = coefficient of x^2 term = 2
b = coefficient of x term = 3
c = constant term = 3
quadratic formula becomes:
x = (-3 plus or minus sqrt(3^2 - 4*2*-2).
this becomes x = (-3 plus or minus sqrt(3^2 + 16)) / 4.
this becomes x = (-3 plus or minus sqrt(25)) / 4.
this becomes x = (-3 plus or minus 5) / 4.
this becomes x = 2/4 or -8/4.
this becomes x = .5 or -2.
to find the factors, set each of these equations equal to 0 as follows:
subtract .5 from both sides of the first value of x to get x - .5 = 0
multiply both sides of that equation to get:
2x - 1 = 0
subtract -2 from both sides of the second value of x to get x + 2 = 0
the factors will be:
(2x - 1) * (x + 2) = 0
multiply these factors together to get:
(2x - 1) * (x + 2) = 2x * (x + 2) - 1 * (x + 2) which becomes:
2x^2 + 4 - x - 2 which becomes:
2x^2 + 3x - 2.
since that is the original equation, the factors look good.
to confirm that they are the factors, replace x with each value.
the equation should be equal to 0.
2x^2 + 3x - 2 becomes 2 * .5^2 + 3 * .5 - 2 when x = .5.
this becomes 2 * .25 - 1.5 + 2 which becomes:
.5 - 1.5 + 2 which becomes 0
2x^2 + 3x - 2 becomes 2 * (-2)^2 + 3 * -2 - 2 when x = -2.
this becomes 2 * 4 - 6 - 2 which becomes:
8 - 6 - 2 hich becomes 0,.
both solution make the equation equal to 0, confirming they are the correct solutions.
with quadratic equations, your fallback position is the quadratic formula.
use of that formula will always provide the solutions, whether they are real or not.
here's a reference on how to solve quadratic equations.
https://www.purplemath.com/modules/solvquad6.htm
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! please help me solve
factorize 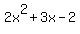
Nothing here to "SOLVE." Plus, you don't have to go through all of what that person went through to Factorize this trinomial
2x2 + 3x - 2
2x2 + 4x - x - 2 ------ Replacing 3x with + 4x - x
2x2 + 4x - x - 2
2x(x + 2) - 1(x + 2)
(2x - 1)(x + 2) <===== Factorized form
That's IT!! Nothing more, nothing less!
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
You can always factor a quadratic expression using the quadratic formula; it is not as much work as the first tutor makes it look.
The solution by the second tutor is fine. But it doesn't teach YOU how to factor the quadratic. For this example, replacing 3x with 4x-x makes the expression factorable using grouping -- but you have no way of knowing that "4x-x" is how you want to replace the "3x". So for a student wanting to learn how to factor the expression, that solution is of little use.
There are many well-defined methods for factoring quadratics. I am definitely old school on this and think the best way to learn to factor quadratics is by looking at the possible factorizations and finding the one that is right.
We want to have

To get the leading term 2x^2, a and c have to be, in some order, 1 and 2.
To get constant term -2, b and d have to be, in some order, 1 and -2, or -1 and 2.
Look at all the possible factorizations and find the one that gives the correct linear term "3x".
(2x+1)(x-2)
(2x-1)(x+2)
(2x+2)(x-1)
(2x-2)(x+1)
Before actually calculating the middle term for each of these possible factorizations, we can rule out the last two. In each of those, the first factor has a common factor of 2, which means the resulting quadratic would have a common factor of 2 -- but it doesn't. So the correct factorization is one of the first two.
The first one gives a middle term of -3x, which is the right size but wrong sign; the second one gives us the correct middle term.
ANSWER: 
|
|
|