Question 1178678: Let a, b, and c be integers that satisfy 2a + 3b = 52, 3b + c = 41, and bc = 60. Find a+b+ c.
Found 3 solutions by MathLover1, greenestamps, josgarithmetic:
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!
 ...........eq.1 ...........eq.1
 ...........eq.2 ...........eq.2
 ...........eq.3 ...........eq.3
-----------------------------
Find 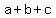
 ...........eq.2, solve for ...........eq.2, solve for 
 ...........eq1) ...........eq1)
 ...........eq.3, solve for ...........eq.3, solve for 
 ................2) ................2)
from 1) and 2) we have
 ........solve for ........solve for 

 ....factor ....factor

solutions:

or

go to
 ...........eq1), substitute ...........eq1), substitute 


or


so we have two pairs of solutions for  and and 
 , ,
and
 , ,
go to
 ...........eq.1, substitute ...........eq.1, substitute 





one solution is:  , , , ,
then 
 ...........eq.1, substitute ...........eq.1, substitute 





other solution is:  , ,  , ,
then 
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
(1) The fastest way to the answer: trial and error with simple mental arithmetic.
Find pairs of integers b and c for which the product bc is 60, then find the pair for which 3b+c=41. Answer b=12, c=5.
Then use 2a+3b=52 with b=12 to find a=8.
And last a+b+c = 8+12+5 = 25.
ANSWER: 25
(2) Using formal algebra....
3b+c=41
c = 41-3b
bc = b(41-3b) = 60
41b-3b^2 = 60
3b^2-41b+60 = 0
Factor into the form
(3b-m)(b-n) = 0
3b^2-(m+3n)+mn=0
We need mn=60 and m+3n=41....
Note that is exactly what we needed in solving the problem using trial and error -- so using the formal algebra didn't make solving the problem easier.
However, assuming this question comes from a formal math course, you should know how to set up and solve the problem using the formal algebra.
Continuing then...
(3b-5)(b-12)=0
b = 5/3 (not an integer) or b=12; so b=12
Then, as before, c=5 and a=8.
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
|
|
|