Question 117703: Find equation of an exponential curve passing through the given pair of points and graph these exponents. Is there any other exponent of the same kind passing through these two points?
A.)(2,12)and(5,96)
B.)(-1,-2/3)and(3,-54)
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website! ): Find equation of an exponential curve passing through the given pair of points and graph these exponents. Is there any other exponent of the same kind passing through these two points?
A.)(2,12)and(5,96)
I'll just do the first one. If I have time, I'll come back and
do the second one too.
The standard exponential function is easy to remember,
because the letters on the right spell the word "pert".
y =  For the point (2, 12), plug in t = 2 and y = 12
12 =
For the point (2, 12), plug in t = 2 and y = 12
12 = 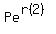 12 =
12 =  y =
y =  For the point (5, 96), plug in t = 5 and y = 96
96 =
For the point (5, 96), plug in t = 5 and y = 96
96 = 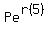 96 =
96 =  Now we have the system of equations:
96 =
Now we have the system of equations:
96 =  12 =
12 =  Write these as
96 =
Write these as
96 =  12 =
12 =  Since equals divided by equals give equals,
the quotient of the left sides equals the
quotient of the right sides:
Since equals divided by equals give equals,
the quotient of the left sides equals the
quotient of the right sides:
 = = 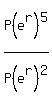 Simplify by dividing on the left, canceling P's
on the right and subtracting exponents on the right:
8 =
Simplify by dividing on the left, canceling P's
on the right and subtracting exponents on the right:
8 = 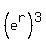 Take cube roots of both sides:
Take cube roots of both sides:
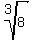 = =  2 =
2 = 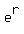 Take the natural logs of both sides:
ln(2) = r
Substitute ln(2) for r in
12 =
Take the natural logs of both sides:
ln(2) = r
Substitute ln(2) for r in
12 =  12 =
12 = 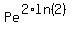 12 =
12 =  12 =
12 = 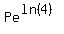 12 =
12 =  12 =
12 =  3 = P
So substituting P = 3 and r = ln(2) into
y =
3 = P
So substituting P = 3 and r = ln(2) into
y =  y =
y = 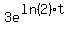 y =
y = 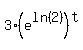 y =
y = 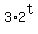 B.)(-1,-2/3)and(3,-54)
Edwin
B.)(-1,-2/3)and(3,-54)
Edwin
|
|
|