SOLUTION: Find a cubic polynomial with integer coefficients that has {{{matrix(2,1,"", 2^(1/3)+4^(1/3)) }}} as a root. I've been working on this question for some time, but I haven'

Algebra ->  Equations -> SOLUTION: Find a cubic polynomial with integer coefficients that has {{{matrix(2,1,"", 2^(1/3)+4^(1/3)) }}} as a root. I've been working on this question for some time, but I haven'      Log On


   

Question 1175454: Find a cubic polynomial with integer coefficients that has 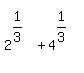matrix%282%2C1%2C%22%22%2C+2%5E%281%2F3%29%2B4%5E%281%2F3%29%29++ as a root.

I've been working on this question for some time, but I haven't made any headway. Can somebody write a solution to this?
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.

See the lesson
    - Prove that the number (cube root of 2 PLUS cube root of 4) is irrational
in this site.

This problem is  ADVANCED  and the solution is intended for  ADVANCED  STUDENTS.
Actually,  it is a  Math  Circle level problem.   Below is the copy of this elegant solution.


Problem

(a)   Find a cubic polynomial with integer coefficients that has 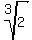  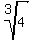root%283%2C2%29 + root%283%2C4%29   as a root.
(b)   Prove that the number 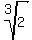  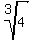root%283%2C2%29 + root%283%2C4%29   is irrational.

Solution

Part (a) 

Let r = 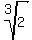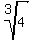root%283%2C2%29 + root%283%2C4%29.


Then,  since  (a+b)^3 = a^3 + 3a^2b + 3ab^2 + b^3 = a^3 + 3ab*(a+b) + b^3


    r^3 = 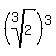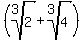%28root%283%2C2%29%29%5E3 + 3%2Aroot%283%2C2%29%2Aroot%283%2C4%29.%28root%283%2C2%29+%2B+root%283%2C4%29%29 + %28root%283%2C4%29%29%5E3 = 

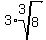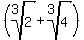        = 2 + 3%2Aroot%283%2C8%29.%28root%283%2C2%29%2Broot%283%2C4%29%29 + 4 = 2 + 3*2*r + 4 = 6 + 6r.


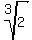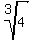It means that  r = root%283%2C2%29 + root%283%2C4%29  is the root to this equation


    r^3 - 6r - 6 = 0.      (*)


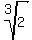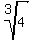ANSWER.   root%283%2C2%29 + root%283%2C4%29  is the root of the cubic polynomial  x^3 - 6x - 6.


Part (a) is solved.



Part (b) 

In part (a), I proved that the number  r = 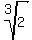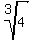root%283%2C2%29 + root%283%2C4%29  is the root of the cubic equation


    x^3 - 6x - 6 = 0.     (**)


Therefore, due to the Rational root theorem, if the number "r" is rational, it must divide the constant term of 6, 
i.e. r must be one of the numbers +/-1, +/-2, +/-3, +/-6.


But it is easy to check that no one of these divisors of 6 IS NOT THE ROOT to equation (**).


Indeed, for these values of x, the values of the polynomial  f(x) = x^3 - 6x -6  are given in the Table


    x       -1      1     -2      2     -3      3     -6     6

    f(x)    -1    -11     -2    -10    -15      3    -186   174


and no one of these values of the polynomial  f(x)  is equal to  0  (zero).

Part  (b)  is solved,  too.


/\/\/\/\/\/\/\/

I am reading the Edwins' comments about my work at this forum,  and can not understand what he wants to say.

Edwin,  don't you think,  that it would be better if you take them back  (or take them off)  and will not comment my posts ?

I have no objections when somebody  (colleagues tutors)  point me to my error (which happens not so often),
moreover,  I always thankful for it . . .

But I always feel myself  UNCOMFORTABLE,  when I see comments,  that I did not deserve  (or that are nonsensical).


                About  @ikleyn job at this forum the visitors and the tutors should know one thing:

                        WHAT  @ikleyn  DOES  at this forum  IS  ALWAYS  RIGHT .



Answer by Edwin McCravy(20055) About Me  (Show Source):
You can put this solution on YOUR website!
We don't turn away "advanced" students if we can solve what they post.  Only
Ikleyn does that. When she does that she removes it from the list of unsolved
problems. That blocks other tutors from seeing the problem unless they visit
the recently solved ones. Luckily I checked that today.  I don't always.

This involves Cardano's cubic formula for the solution to x³+px+q=0, which is
not all that advanced. It only involves roots, which anyone in pre-calc can handle.

Cardano's formula for the solution for x³+px+q=0 is

x%22%22=%22%22root%283%2C-q%2F2%2Bsqrt%28q%5E2%2F4%2Bp%5E3%2F27%29%29%22%22%2B%22%22root%283%2C-q%2F2-sqrt%28q%5E2%2F4%2Bp%5E3%2F27%29%29 

matrix%282%2C1%2C%22%22%2C+2%5E%281%2F3%29%2B4%5E%281%2F3%29%29++matrix%282%2C1%2C%22%22%2C%22%22=%22%22%29matrix%282%2C1%2C%22%22%2Croot%283%2C2%29%2Broot%283%2C4%29%29

So we try to find p and q so that what's under one cube root equals 2 and
what's under the other one equals 4.

So set -q%2F2%2Bsqrt%28q%5E2%2F4%2Bp%5E3%2F27%29 equal to 2 and it will simplify to
an equation in p3 and q.

Then set -q%2F2-sqrt%28q%5E2%2F4%2Bp%5E3%2F27%29 equal to 4 and it will also simplify to
an equation in p3 and q.

Then from those two equations, you can find integers for p and q.

Then the answer will be x3 + px + q.

If you need more help, ask for it in the form below, and I'll get back to you
by email.

Edwin