SOLUTION: Manuel bought 6 candy bars and 3 sodas at the gas station for $8.40. Gary bought 3 candy bars and 4 sodas at the same gas station for $7.45. What is the price of one soda?

Click here to see ALL problems on Equations

Question 1173102: Manuel bought 6 candy bars and 3 sodas at the gas station for $8.40. Gary bought 3 candy bars and 4 sodas at the same gas station for $7.45. What is the price of one soda?
Found 4 solutions by josgarithmetic, greenestamps, MathTherapy, ikleyn:
Answer by josgarithmetic(39616)   (Show Source):
You can put this solution on YOUR website!

.

.

Answer by greenestamps(13198)   (Show Source):
You can put this solution on YOUR website!

The suggested solution method shown by the other tutor will not lead to a correct answer, since it contains a simple arithmetic error.

Manuel bought 6 candy bars and 3 sodas for $8.40
Gary bought 3 candy bars and 4 sodas for $7.45

some third person bought exactly twice as much as Gary, so paid exactly twice as much

The difference between the first and third purchases is 5 more sodas, for a difference of $6.50

The cost of each soda is $1.30

Using Manuel's purchase and the now known cost of each soda to determine the cost of each candy bar

ANSWERS: Each soda costs $1.30; each candy bar costs $0.75

Answer by MathTherapy(10551)   (Show Source):
You can put this solution on YOUR website!

Manuel bought 6 candy bars and 3 sodas at the gas station for $8.40. Gary bought 3 candy bars and 4 sodas at the same gas station for $7.45. What is the price of one soda?

Let cost of each candy bar, and soda, be C and S, respectively
Then we get: 6C + 3S = 8.4 ------- eq (i)
Also, 3C + 4S = 7.45 -------- eq (ii)
6C + 8S = 14.9 ------- Multiplying eq (ii) by 2 ------ eq (iii)
5S = 6.5 ------- Subtracting eq (i) from eq (iii)
Cost of a soda, or

Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website!
.

The equations are 6x + 3y = 840 cents 3x + 4y = 745 cents I will apply the determinant method (= the Cramers' rule) to find y, the soda's price. y = 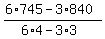= 130. ANSWER. The soda's price is $1.30.

Solved.

-------------

I never use a pocket calculator.

I use Excel. I copy the formula into Excel and get the answer in one click (and with no error).

            Side note. By the way, in engineering companies in US, where I worked for many years
            and where the engineers made thousands calculations every day, I did not see anyone
            who used pocket calculators - the engineers simply have no such a "luxury" to work so slowly.

            All handle calculations were made in Excel. Honestly, working at their regular rate/charge/duties,
            the engineers simply HAVE NO TIME to lend a hand for a pocket calculator . . .

            So, for me, calculators are comparable with the old typing machines, that all are now out
            of use just 20 or 30 years. // New generations of students just do not know what they were . . .

If you have no Excel in your computer, you can use free of charge online calculator www.desmos.com

In the same way as with Excel, you can copy (or type) the entire formula in this online calculator
and get the answer in one click.

================

On the Determinants' method for solving the systems of two linear equations in two unknowns see the lesson
    - Solution of the linear system of two equations in two unknowns using determinant
in this site.

Also, you have this free of charge online textbook in ALGEBRA-I in this site
    - ALGEBRA-I - YOUR ONLINE TEXTBOOK.

The referred lesson is the part of this online textbook under the topic "Systems of two linear equations in two unknowns".

Save the link to this online textbook together with its description

Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson

to your archive and use it when it is needed.