Question 1172154: 3. What is the value of k that will make the trinomial 64x2 + 56x + k be a perfect square? Show clear solution thanksss!
Found 3 solutions by ikleyn, math_tutor2020, MathTherapy:
Answer by ikleyn(52780)   (Show Source): (Show Source):
Answer by math_tutor2020(3816)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Consider the perfect square trinomial formula
(a+b)^2 = a^2 + 2ab + b^2
The expression 64x^2+56x+k has three terms, as does the right hand side of the equation above.
Equating the two expressions shows that
64x^2 = a^2
56x = 2ab
k = b^2
To find k, we'll need to figure out b.
To figure out b, we need to find 'a' first
If 64x^2 = a^2, then
a^2 = 64x^2
a^2 = (8x)^2
a = 8x
where the last step has us apply the square root to both sides.
We could end up with a = -8x, but this value will ultimately lead to the same value of k. So we'll stick to a = 8x to make things simple.
Use that value of 'a', and the second equation we formed, to get
56x = 2ab
56x = 2(8x)b
56x = 16xb
56 = 16b
16b = 56
b = 56/16
b = (8*7)/(8*2)
b = 7/2
Note: if you went with a = -8x, then b = -7/2. Otherwise, b is positive.
Now we can compute k
k = b^2
k = (7/2)^2
k = (7^2)/(2^2)
k = 49/4
This means 64x^2+56x+k updates to 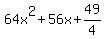 which factors to which factors to 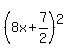 . .
Use the perfect square trinomial formula template, given at the very top of the solution, to help factor.
Because we can rewrite 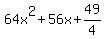 into the form (expression)^2, this proves into the form (expression)^2, this proves 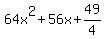 is a perfect square trinomial. is a perfect square trinomial.
-------------------------------------------------------
Answer: 49/4
In decimal form, this is exactly 49/4 = 12.25
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! 3. What is the value of k that will make the trinomial 64x2 + 56x + k be a perfect square? Show clear solution thanksss!
You just need to COMPLETE the SQUARE, as follows: 
Therefore, as seen above, 
|
|
|