SOLUTION: Find the quadratic equation in x with the given roots 1±3i√5 / 2 <- (it is a fraction). Show clear solution thanksss!

Algebra ->  Equations -> SOLUTION: Find the quadratic equation in x with the given roots 1±3i√5 / 2 <- (it is a fraction). Show clear solution thanksss!      Log On


   

Question 1172153: Find the quadratic equation in x with the given roots 1±3i√5 / 2 <- (it is a fraction). Show clear solution thanksss!
Found 2 solutions by math_tutor2020, MathTherapy:
Answer by math_tutor2020(3816) About Me  (Show Source):
You can put this solution on YOUR website!

Use the zero product property to help go from the given roots to a quadratic polynomial.

x+=+%281%2B3i%2Asqrt%285%29%29%2F2 or x+=+%281-3i%2Asqrt%285%29%29%2F2

2x+=+1%2B3i%2Asqrt%285%29 or 2x+=+1-3i%2Asqrt%285%29 Multiply both sides by 2

2x-1+=+3i%2Asqrt%285%29 or 2x-1+=+-3i%2Asqrt%285%29 Subtract 1 from both sides

%282x-1%29%5E2+=+%283i%2Asqrt%285%29%29%5E2 or %282x-1%29%5E2+=+%28-3i%2Asqrt%285%29%29%5E2 Square both sides

%282x-1%29%5E2+=+9i%5E2%2A5

%282x-1%29%5E2+=+9%28-1%29%2A5 Use i^2 = -1

%282x-1%29%5E2+=+-45

%282x-1%29%5E2%2B45+=+0

4x%5E2-4x%2B1%2B45+=+0 FOIL

4x%5E2-4x%2B46+=+0

2%282x%5E2-2x%2B23%29+=+0

2x%5E2-2x%2B23+=+0%2F2

2x%5E2-2x%2B23+=+0 This is the final answer.

-------------------------------------------------------------------

We can use the quadratic formula to confirm this

For 2x%5E2-2x%2B23+=+0, we have a = 2, b = -2, c = 23

x+=+%28-b%2Bsqrt%28b%5E2-4ac%29%29%2F%282a%29 or x+=+%28-b-sqrt%28b%5E2-4ac%29%29%2F%282a%29

x+=+%28-%28-2%29%2Bsqrt%28%28-2%29%5E2-4%282%29%2823%29%29%29%2F%282%282%29%29 or x+=+%28-%28-2%29-sqrt%28%28-2%29%5E2-4%282%29%2823%29%29%29%2F%282%282%29%29

x+=+%282%2Bsqrt%28-180%29%29%2F%282%282%29%29 or x+=+%282-sqrt%28-180%29%29%2F%282%282%29%29

x+=+%282%2Bsqrt%2836%2A%28-1%29%2A5%29%29%2F%282%282%29%29 or x+=+%282-sqrt%2836%2A%28-1%29%2A5%29%29%2F%282%282%29%29

x+=+%282%2Bsqrt%2836%29%2Asqrt%28-1%29%2Asqrt%285%29%29%2F%282%282%29%29 or x+=+%282-sqrt%2836%29%2Asqrt%28-1%29%2Asqrt%285%29%29%2F%282%282%29%29

x+=+%282%2B6i%2Asqrt%285%29%29%2F%282%282%29%29 or x+=+%282-6i%2Asqrt%285%29%29%2F%282%282%29%29

x+=+%282%281%2B3i%2Asqrt%285%29%29%29%2F%282%282%29%29 or x+=+%282%281-3i%2Asqrt%285%29%29%29%2F%282%282%29%29

x+=+%281%2B3i%2Asqrt%285%29%29%2F2 or x+=+%281-3i%2Asqrt%285%29%29%2F2

We end up with the roots that were given to us. So this confirms that 2x%5E2-2x%2B23 has the proper roots we were given. In other words, this confirms that the given roots lead to 2x%5E2-2x%2B23

Note: we could scale both sides of 2x%5E2-2x%2B23+=+0 by some nonzero number k, and get the same roots (since we can undo this and divide both sides by k). To keep things fairly simple, we'll make k = 1. We can consider 2x%5E2-2x%2B23 to be reduced as much as possible since the coefficients 2,-2,23 only have the common factor 1 between them.

-------------------------------------------------------------------

Answer: 2x%5E2-2x%2B23+=+0


Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!
Find the quadratic equation in x with the given roots 1±3i√5 / 2 <- (it is a fraction). Show clear solution thanksss!
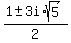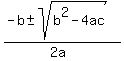
%281+%2B-+3i%2Asqrt%285%29%29%2F2 ====> %28-+b+%2B-+sqrt%28b%5E2+-+4ac%29%29%2F%282a%29

As seen above, and based on the quadratic equation formula, 1 = - b___b = - 1

Also, as seen above, and based on the quadratic equation formula, matrix%283%2C3%2C+2%2C+%22=%22%2C+2a%2C+2%2F2%2C+%22=%22%2C+a%2C+1%2C+%22=%22%2C+a%29

                                                                  

Finally, as seen above, and based on the quadratic equation formula, the DISCRIMINANT, matrix%281%2C3%2C+b%5E2+-+4ac%2C+%22=%22%2C+-+45%29

                                                                  

                                                                  matrix+%281%2C3%2C+ax%5E2+%2B+bx+%2B+c%2C+%22=%22%2C+0%29 <====== General form of a quadratic equation

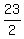                                                                  matrix+%281%2C3%2C+x%5E2+-+x+%2B+23%2F2%2C+%22=%22%2C+0%29 -------- Substituting 1 for a, - 1 for b, and 23%2F2 for c.

                                                                  h+ighlight_green%28matrix%281%2C3%2C+2x%5E2+-+2x+%2B+23%2C+%22=%22%2C+0%29%29 ----- Multiplying the above by LCD, 2