Question 1172123: For what value(s) of k will x^2+4x+4 be a factor of: f(x)= x^4−18x^2+kx+44
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Notice that 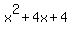 = =  .
Therefore, if the trinomial .
Therefore, if the trinomial 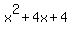 divides the polynomial f(x)= divides the polynomial f(x)=  with no remainder,
it implies that the binomial (x+2) divides this polynomial with no remainder.
In turn, due to the Remainder theorem, it means that x= -2 is the root of the polynomial f(x).
So, we substitute x= -2 into the polynomial f(x) and equate it to zero
f(-2) = with no remainder,
it implies that the binomial (x+2) divides this polynomial with no remainder.
In turn, due to the Remainder theorem, it means that x= -2 is the root of the polynomial f(x).
So, we substitute x= -2 into the polynomial f(x) and equate it to zero
f(-2) = 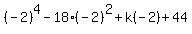 = -12 - 2k = 0.
It gives us a linear equation for k, which leads to
2k = -12,
k = -12/2 = -6.
At this point, we obtain the following result
+-----------------------------------------------------------------+
| if the trinomial x^2+4x+4 divides the polynomial |
| |
| f(x)= x^4-18x^2+kx+44 with no remainder, then k= -6. |
+-----------------------------------------------------------------+
But the direct check shows that
+-----------------------------------------------------------------+
| the trinomial x^2+4x+4 DOES NOT divide the polynomial |
| |
| f(x)= x^4-18x^2-6x+44 with no remainder |
+-----------------------------------------------------------------+
Hence, the value of "k" satisfying the given condition DOES NOT EXIST.
ANSWER. The value of "k" satisfying the given condition DOES NOT EXIST. = -12 - 2k = 0.
It gives us a linear equation for k, which leads to
2k = -12,
k = -12/2 = -6.
At this point, we obtain the following result
+-----------------------------------------------------------------+
| if the trinomial x^2+4x+4 divides the polynomial |
| |
| f(x)= x^4-18x^2+kx+44 with no remainder, then k= -6. |
+-----------------------------------------------------------------+
But the direct check shows that
+-----------------------------------------------------------------+
| the trinomial x^2+4x+4 DOES NOT divide the polynomial |
| |
| f(x)= x^4-18x^2-6x+44 with no remainder |
+-----------------------------------------------------------------+
Hence, the value of "k" satisfying the given condition DOES NOT EXIST.
ANSWER. The value of "k" satisfying the given condition DOES NOT EXIST.
Solved, answered, explained and completed.
|
|
|