SOLUTION: Consider the integers x and y . When y is divided by x the remainder is 29. When y is divided by x/2, the remainder is 13. Determine x

(1)  Consider the statement "When y is divided by x the remainder is 29".


     It means that there is an integer number "n" such that

        y = nx + 29,   29 < x.         (1)



(2)  Consider next statement "When y is divided by x/2, the remainder is 13".


     It means that there is an integer number "m" such that

        y = 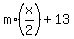,   13 < .     (2)



(3)  From equations (1) and (2)  we have

        nx + 29 = 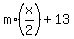,    x > 29   


     or, equivalently

        2nx + 58 = mx + 26,     x > 29

        58 - 26  = mx - 2nx,    x > 29

        32       = (m - 2n)x,   x > 29      (3)



(4)  Thus, the integer number  x  is a divisor of the number 32, and x > 29.


     But the only such integer is  x = 32.